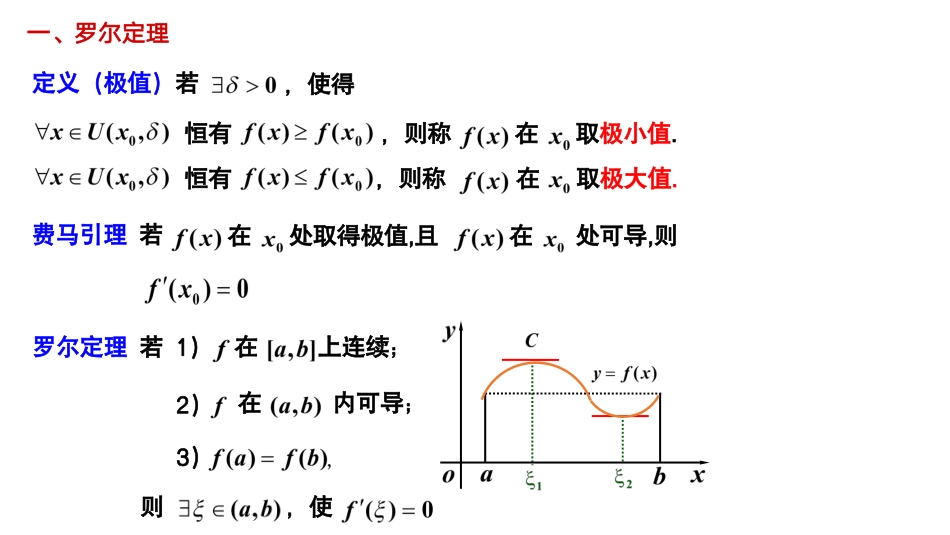
第三章微分中值定理与导数应用第一节微分中值定理主讲武忠祥教授一、罗尔定理定义(极值)若,使得恒有,则称在取极小值.恒有,则称在取极大值.费马引理若在处取得极值,且在处可导,则罗尔定理若1)在上连续;在内可导;则,使2)3)费马(1601–1665)费马法国数学家,他是一位律师,数学只是他的业余爱好.他兴趣广泛,博览群书并善于思考,在数学上有许多重大贡献.他特别爱好数论,他提出的费马大定理:历经358年,直到1993年才由美国普林斯顿大学的安德鲁.怀尔斯教授经过十年的潜心研究才得到解决.引理是后人从他研究解决最值的方法中提炼出来的.二、拉格朗日中值定理拉格朗日中值定理若在上连续;2)内可导,1)在,使则注:1)结论都成立.2)有限增量公式推论设在区间上连续,在内可导,则在上拉格朗日(1736-1813)法国数学家.他在方程论,解析函数论,及数论方面都作出了重要的贡献,近百余年来,数学中的许多成就都可直接或间接地追溯到他的工作,他是对分析数学产生全面影响的数学家之一.例1试证例2证明:当时,例3证明:当时,三、柯西中值定理柯西中值定理若上连续;在内可导,且1)2)在则,使内容小结1.意义2.关系3.应用(1)证明恒等式(2)证明不等式(3)证明有关中值问题的结论建立局部和整体的关系罗尔定理拉格朗日中值定理柯西中值定理作业P132:5;6;7;8;10;11;12.