1.3 空间直角坐标及空间向量运算的坐标表示（课件）-【上好数学课】2020-2021学年高二同步备课系列（人教A版2019选择性必修一）.pptxVIP免费

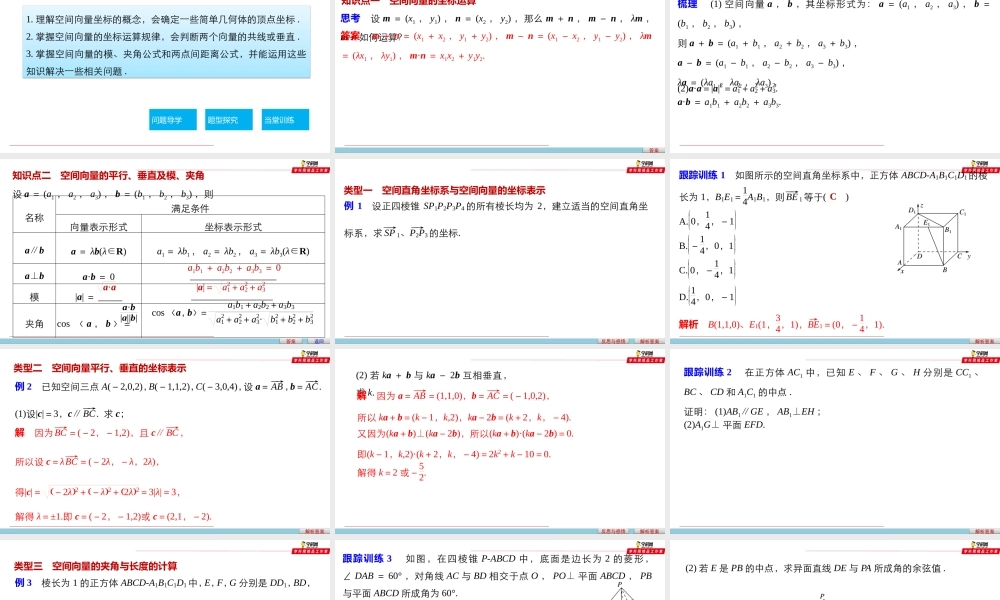
第一章1.3空间向量及其运算的坐标表示学科网1.理解空间向量坐标的概念，会确定一些简单几何体的顶点坐标.2.掌握空间向量的坐标运算规律，会判断两个向量的共线或垂直.3.掌握空间向量的模、夹角公式和两点间距离公式，并能运用这些知识解决一些相关问题.问题导学题型探究当堂训练学习目标知识点一空间向量的坐标运算答案问题导学思考设m＝(x1，y1)，n＝(x2，y2)，那么m＋n，m－n，λm，m·n如何运算？答案m＋n＝(x1＋x2，y1＋y2)，m－n＝(x1－x2，y1－y2)，λm＝(λx1，λy1)，m·n＝x1x2＋y1y2.梳理(1)空间向量a，b，其坐标形式为：a＝(a1，a2，a3)，b＝(b1，b2，b3)，则a＋b＝(a1＋b1，a2＋b2，a3＋b3)，a－b＝(a1－b1，a2－b2，a3－b3)，λa＝(λa1，λa2，λa3)，a·b＝a1b1＋a2b2＋a3b3.(2)a·a＝|a|2＝a21＋a22＋a23.名称满足条件向量表示形式坐标表示形式a∥ba＝λb(λ∈R)a1＝λb1，a2＝λb2，a3＝λb3(λ∈R)a⊥ba·b＝0__________________模|a|＝______________________夹角cos〈a，b〉＝知识点二空间向量的平行、垂直及模、夹角答案设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则a·a|a|＝a21＋a22＋a23a·b|a||b|cos〈a，b〉＝a1b1＋a2b2＋a3b3a21＋a22＋a23·b21＋b22＋b23a1b1＋a2b2＋a3b3＝0返回解析答案类型一空间直角坐标系与空间向量的坐标表示题型探究反思与感悟例1设正四棱锥SP1P2P3P4的所有棱长均为2，建立适当的空间直角坐标系，求SP―→1、P2P―→3的坐标.跟踪训练1如图所示的空间直角坐标系中，正方体ABCD-A1B1C1D1的棱长为1，B1E1＝14A1B1，则BE―→1等于()A.0，14，－1B.－14，0，1C.0，－14，1D.14，0，－1解析答案解析B(1,1,0)、E1(1，34，1)，BE→1＝(0，－14，1).C类型二空间向量平行、垂直的坐标表示解析答案例2已知空间三点A(－2,0,2)，B(－1,1,2)，C(－3,0,4)，设a＝AB―→，b＝AC―→.(1)设|c|＝3，c∥BC―→.求c；解因为BC―→＝(－2，－1,2)，且c∥BC―→，所以设c＝λBC―→＝(－2λ，－λ，2λ)，得|c|＝－2λ2＋－λ2＋2λ2＝3|λ|＝3，解得λ＝±1.即c＝(－2，－1,2)或c＝(2,1，－2).解析答案反思与感悟(2)若ka＋b与ka－2b互相垂直，求k.解因为a＝AB―→＝(1,1,0)，b＝AC―→＝(－1,0,2)，所以ka＋b＝(k－1，k,2)，ka－2b＝(k＋2，k，－4).又因为(ka＋b)⊥(ka－2b)，所以(ka＋b)·(ka－2b)＝0.即(k－1，k,2)·(k＋2，k，－4)＝2k2...