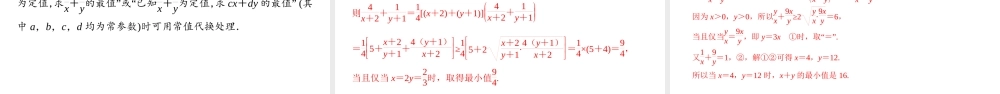2.2基本不等式第2课时基本不等式的综合应用学习目标素养目标学科素养1.能够运用基本不等式解决生活中的最值问题(难点);2.能够对式子进行变形,构造定值;3.会用基本不等式解决恒成立问题(重点)。1、数学运算2、逻辑推理3、数学建模自主学习一.基本不等式与最值已知x、y都是正数,1.若积xy等于定值P,那么当x=y时,和x+y有最小值_____.2.若和x+y是定值S,那么当x=y时,积xy有最大值_____.自主学习二.运用基本不等式求最值的三个条件:正数定值1.“一正”:x,y必须是;2.“二定”:求积xy的最大值时,应看和x+y是否为;求和x+y的最小值时,应看积xy是否为.3.“三相等”:当且仅当x=y时,等号成立。定值自主学习三.通过变形构造定值的方法如果题目中基本不等式不能满足“和为定值”或“积为定值”,就不能直接用基本不等式求最值。需要通过变形,构造定值,常见方法有:配项法;配系数法;分式型基本不等式;常值代换法“1”的代换。1.思辨解析(正确的打“√”,错误的打“×”)(1)任意的正数ab、,且1ab,都有2ab.()(2)若ab=2,则a+b的最小值为22.()(3)当x>1时,函数y=x+1x-1≥2xx-1,所以函数y的最小值是2xx-1.()(4)若x∈R,则x2+2+1x2+2≥2.()2.若x>0,则x+2x的最小值是________.小试牛刀×√××22解析:x+2x≥2x·2x=22,当且仅当x=2时,等号成立.题型一利用基本不等式求最值经典例题例1当x>0时,y=12x+4x的最小值为()A.4B.8C.83D.16C解析: x>0,∴12x>0,4x>0.∴y=12x+4x≥212x·4x=83.当且仅当12x=4x,即x=3时取最小值83,∴当x>0时,y的最小值为83.跟踪训练1经典例题已知x<0,求221xxy最大值。思路点拨:利用基本不等式求最值要满足“一正”、“二定”、“三相等”,现在x<0,021x,通过变形221xxy再利用基本不等式求最值。解: x<0,∴通过变形, ∴当且仅当,即时,等号成立,取得最大值。题型一利用基本不等式求最值经典例题题型二变形构造定值—配项法解:通过配项得;当且仅当111xx,即x=2时,等号成立,取得最小值3.例2当x>1时,求函数y=x+1x-1最小值。经典例题总结以拼凑出和是定值或积是定值的形式为目标,根据代数式的结构特征,利用系数的变化或对常数的调整进行巧妙变形,注意做到等价变形.一般地,形如f(x)=ax+b+ecx+d的函数求最值时可以考虑配凑法.题型二变形构造定值—配项法跟踪训练2经典例题若x<3,则实数f...