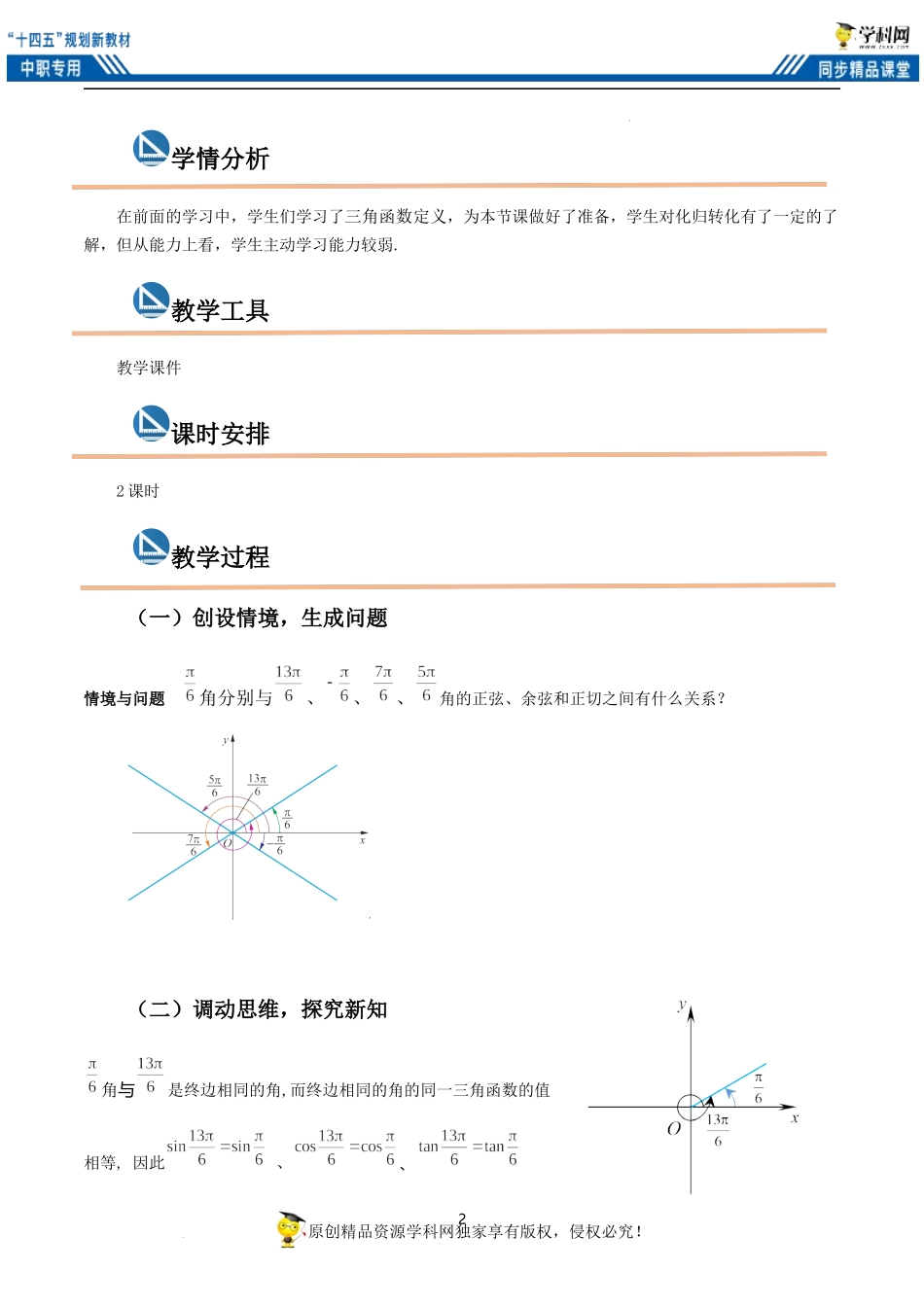
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司《4.5诱导公式一》教学设计学习目标学习重难点教材分析本节课是学习了三角函数定义后,利用三角函数定义导出三角函数四组公式,并通过运用这些公式,把求任意角的三角函数值转化为求锐角的三角函数值,从而渗透了把未知问题化归为已知问题的思想.知识能力与素养知道角“”、“”与的终边之间的关系.(1)会利用简化公式将任意角的三角函数的转化为锐角的三角函数;(2)会利用计算器求任意角的三角函数值;(3)培养学生的数学思维能力及应用计算工具的能力.重点难点诱导公式.诱导公式的应用.2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学情分析在前面的学习中,学生们学习了三角函数定义,为本节课做好了准备,学生对化归转化有了一定的了解,但从能力上看,学生主动学习能力较弱.教学工具教学课件课时安排2课时教学过程(一)创设情境,生成问题情境与问题角分别与、、、角的正弦、余弦和正切之间有什么关系?(二)调动思维,探究新知角与是终边相同的角,而终边相同的角的同一三角函数的值相等,因此、、3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司角与角的终边关于x轴对称,由三角函数的单位圆定义可得,、、下面借助单位圆的对称性进一步研究任意角的正弦、余弦和正切值之间的关系.1.角2k+(kZ)与角的三角函数值之间的关系由三角函数的定义可知,终边相同的角的同一三角函数值相等.即sin(2k+)=sin;cos(2k+)=cos;tan(2k+)=tan.由公式可以将任意角的三角函数值转化为[0,2π)内的角的三角函数值.2.角−与角的三角函数值之间的关系角α和角−α的终边边关于x轴对称,设它们的终边与单位圆的交点分别是点P和P;又由同角三角函数间的关系式,得到:sin(−)=−sin;cos(−)=cos;tan(−)=−tan.由公式可将负角的三角函数转化为正角的三角函数.诱导公式一:sin(2k+)=sin;cos(2k+)=cos;tan(2k+)=tan.诱导公式二:sin(−)=−sin;cos(−)=cos;tan(−)=−tan.【设计意图】结合单位圆和三角函数的定义对两组公式中的角数的位置关系以及终边上与单位圆交点坐标的关系进行分析,学生通过观察、分析和比较可以自己得出诱导公式,体验知识探索的全过程.(三)巩固知识,典例练习【典例1】求下列三角函数值.(1)sin780°;(2);(3...