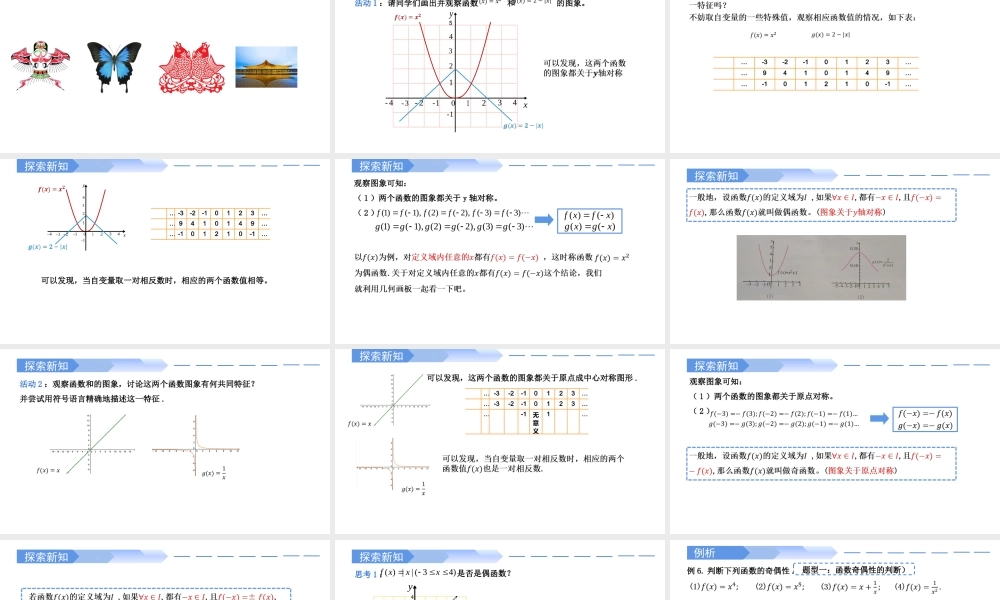
3.2函数的基本性质3.2.2奇偶性情境导入探索新知活动1:请同学们画出并观察函数和的图象。x01-2-3-4-1-123234415y探索新知…-3-2-10123……9410149……-101210-1…探索新知x01-2-3-4-1-12323441y…-3-2-10123……9410149……-101210-1…可以发现,当自变量取一对相反数时,相应的两个函数值相等。探索新知观察图象可知:(1)两个函数的图象都关于y轴对称。(2))()(xgxg)()(xfxf)3()3(),2()2(),1()1(ffffff)3()3(),2()2(),1()1(gggggg探索新知探索新知活动2:观察函数和的图象,讨论这两个函数图象有何共同特征?并尝试用符号语言精确地描述这一特征.探索新知可以发现,这两个函数的图象都关于原点成中心对称图形.…-3-2-10123……-3-2-10123……-1无意义1…探索新知观察图象可知:(1)两个函数的图象都关于原点对称。(2)探索新知探索新知思考1:是否是偶函数?)43(||)(xxxf••xy01-2-3-4-1-2-12341234)43(||)(xxxf也就是说明偶函数的定义域一定要关于原点对称。(奇函数也是)例析例6.判断下列函数的奇偶性.题型一:函数奇偶性的判断)例析求定义域并判断是否关于原点对称下结论例6.判断下列函数的奇偶性.(题型一:函数奇偶性的判断)探索新知练习题型二:利用函数奇偶性求参数练习答案:(1)4;(2)-1.练习题型三:利用函数奇偶性求分段函数的解析式练习练习题型四:比较大小(奇偶性与单调性的综合)练习题型四:比较大小(奇偶性与单调性的综合)解题技巧:(1)若自变量在同一区间内,直接利用函数的单调性比较大小;(2)若自变量不在同一区间内,需利用函数的奇偶性把自变量转化的同一区间内,再利用单调性比较大小.练习题型五:解不等式问题(奇偶性与单调性的综合)题型五:解不等式问题(奇偶性与单调性的综合)练习练习课堂小结&作业小结:1.偶函数、奇函数的定义及其几何意义;2.判断奇偶函数的思路;3.各题型的注意事项.作业:1.课本P851、2、3题;2.课本习题3.2的5、11、12题