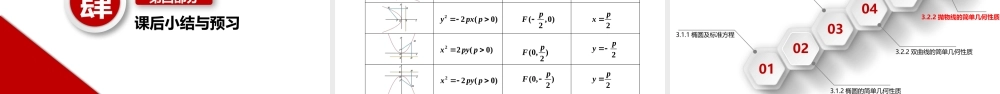3.3.1抛物线及其标准方程（课件）-2022-2023学年高二数学同步名师精讲课件（圆锥曲线篇人教A版2019选择性必修第一册）.pptxVIP免费

3.3.1抛物线及其标准方程ConicSection第三章圆锥曲线的方程抛物线也是具有广泛应用的一种圆锥曲线，如拱桥、导弹飞行轨迹等都要用到抛物线线的性质.本节我们将类比椭圆、双曲线的研究过程与方法研究抛物线的有关问题.目录CONTENTS1234探究抛物线的轨迹及定义抛物线的标准方程典型例题及课堂练习课后小结与预习壹第一部分探究抛物线的轨迹及定义第一部分探究利用信息技术作图.如图3.3-1,F是定点，L是不经过点F的定直线，H是直线l上任意一点，过点l作MH⊥L,线段FH的垂直平分线m交MH于点M.施动点H,观察点M的轨迹，它是什么形状？你能发现点M满足的几何条件吗？可以发现,点M的轨迹形状与二次函数的图象相似.在点M随着点H运动的过程中，始终有ǀMFǀ=ǀMHǀ,即点M与定点F的距离等于它到定直线l的距离.我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线(parabola).点F叫做抛物线的焦点，直线l叫做抛物线的准线.贰第二部分抛物线的标准方程比较椭圆双曲线标准方程的建立过程，你认为如何建立坐标系可能使所求抛物线的方程形式简单？第二部分根据抛物线的几何特征,如图3.3-2,我们取经过点F且垂直于直线l的直线为x轴，垂足为K,并使原点与线段KF的中点重合，建立平面直角坐标系Oxy.设|KF|=p(p>0),那么焦点F的坐标为，准线l的方程为.(,0)2p2pxKFM••xyO图3.3-2H设M(x,y)是抛物线上任意一点，点M到准线l的距离为d.由抛物线的定义，抛物线是点的集合P={MǀǀMFǀ=d}.将上式两边平方并化简,得y2=2px(p>0).①22(),22ppMFxydx22()22ppxyx2px从上述过程可以看到,抛物线上任意一点的坐标(x,y)都是方程①的解,以方程①的解为坐标的点(x,y)与抛物线的焦点的距离和它到准线的距离相等,即以方程①的解为坐标的点都在抛物线上,我们把方程①叫做抛物线的标准方程,它表示焦点在x轴正半轴上,焦点是，准线是(,0)2pF(,0)2pF2px第二部分设M(x,y)是抛物线上任意一点，点M到准线l的距离为d.由抛物线的定义，抛物线是点的集合P={MǀǀMFǀ=d}.将上式两边平方并化简,得y2=2px(p>0).①22(),22ppMFxydx22()22ppxyxKFM••xyOH第二部分KFM••xyOHKFM••xyOHKFM••xyOHKFM••xyOH四种不同的建立平面直角坐标系第二部分在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同形式的标准方程,抛物线的标准方程有哪些不同的形式?请探究之后填写下表.图像标准方程焦点坐标准线方程2px...