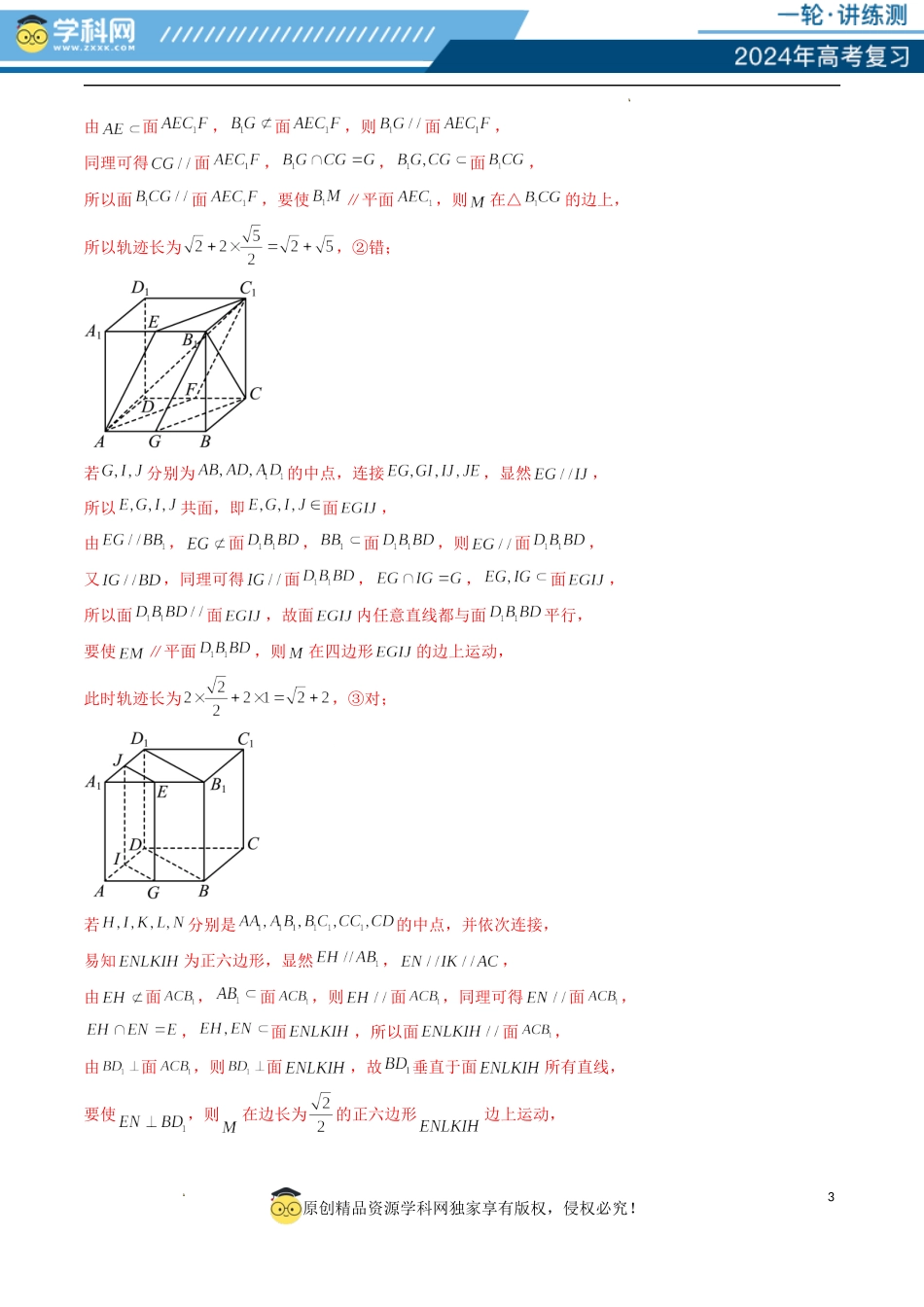
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司重难点突破04立体几何中的轨迹问题目录立体几何中的轨迹问题常用的五种方法总结:1、定义法2、交轨法3、几何法4、坐标法5、向量法题型一:由动点保持平行求轨迹例1.(2023·贵州铜仁·高二贵州省铜仁第一中学校考开学考试)设正方体的棱长为1,点E是棱的中点,点M在正方体的表面上运动,则下列命题:2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司①如果,则点M的轨迹所围成图形的面积为;②如果∥平面,则点M的轨迹所围成图形的周长为;③如果∥平面,则点M的轨迹所围成图形的周长为;④如果,则点M的轨迹所围成图形的面积为.其中正确的命题个数为()A.1B.2C.3D.4【答案】C【解析】由面,而面,则,又,又,面,则面,由面,则,同理,,面,则面,所以垂直于面所有直线,且面,若,则在边长为的正△的边上,故轨迹图形面积为,①对;若分别为中点,连接,由正方体的性质易得,,所以共面,且为平行四边形,故面即为面,3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司由面,面,则面,同理可得面,,面,所以面面,要使∥平面,则在△的边上,所以轨迹长为,②错;若分别为的中点,连接,显然,所以共面,即面,由,面,面,则面,又,同理可得面,,面,所以面面,故面内任意直线都与面平行,要使∥平面,则在四边形的边上运动,此时轨迹长为,③对;若分别是的中点,并依次连接,易知为正六边形,显然,,由面,面,则面,同理可得面,,面,所以面面,由面,则面,故垂直于面所有直线,要使,则在边长为的正六边形边上运动,4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司所以轨迹图形面积为,④对;故选:C例2.(2023·辽宁沈阳·高一沈阳二十中校联考期末)在棱长为1的正方体中,E在棱上且满足,点F是侧面上的动点,且面AEC,则动点F在侧面上的轨迹长度为.【答案】【解析】如图,取的中点,并连接、、,因为E在棱上且满足,即E是棱的中点,所以,又平面,平面,所以平面,同理可证平面,又,所以平面平面,又平面,所以平面,所以动点F在侧面上的轨迹即为,因为正方体的棱长为1,由勾股定理有:.故答案为:.例3.(2023·福建福州·高一福建省福州屏东中学校考期末...