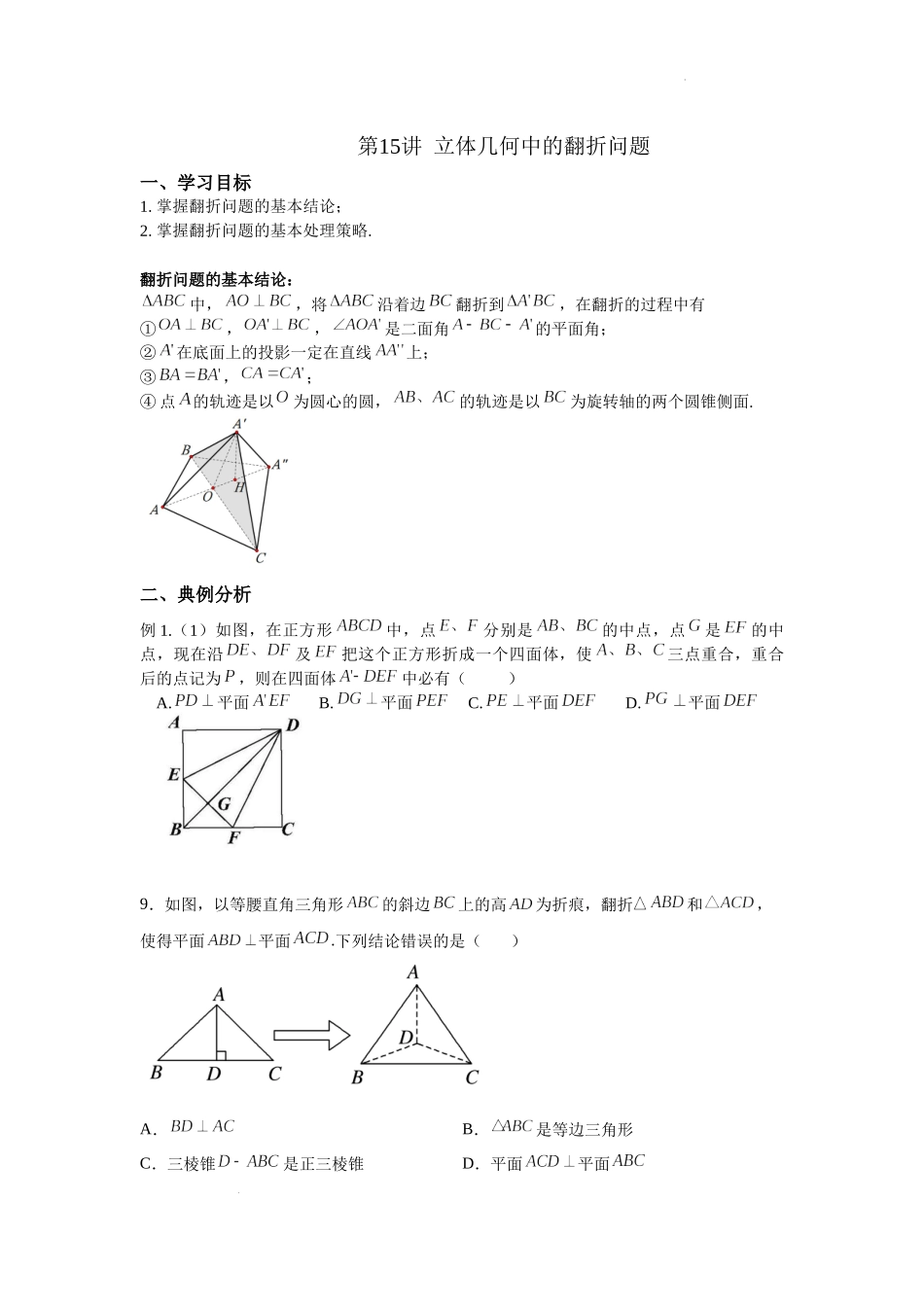
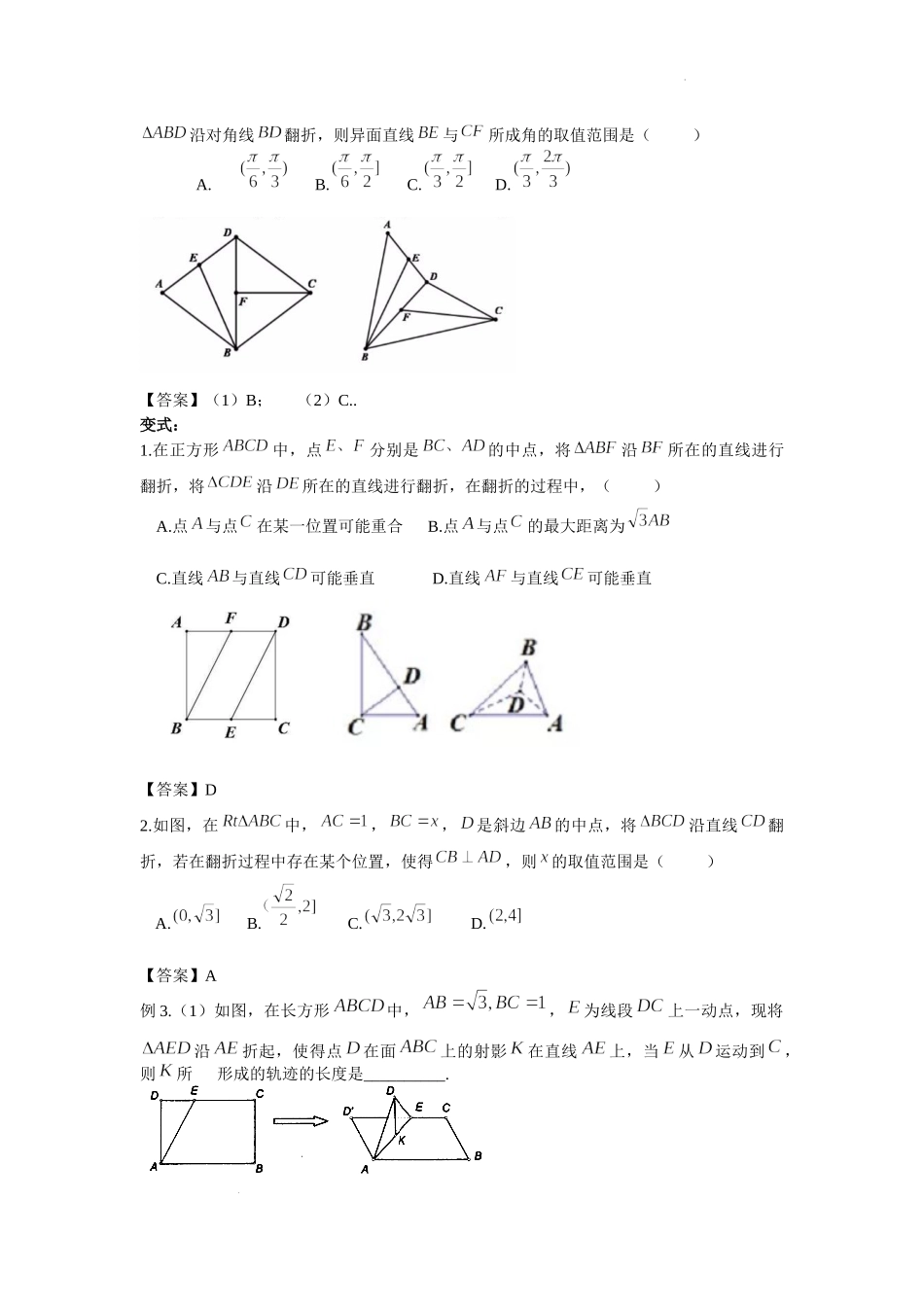
学科网(北京)股份有限公司第15讲立体几何中的翻折问题一、学习目标1.掌握翻折问题的基本结论;2.掌握翻折问题的基本处理策略.翻折问题的基本结论:中,,将沿着边翻折到,在翻折的过程中有①,,是二面角的平面角;②在底面上的投影一定在直线上;③,;④点的轨迹是以为圆心的圆,的轨迹是以为旋转轴的两个圆锥侧面.二、典例分析例1.(1)如图,在正方形中,点分别是的中点,点是的中点,现在沿及把这个正方形折成一个四面体,使三点重合,重合后的点记为,则在四面体中必有()A.平面B.平面C.平面D.平面9.如图,以等腰直角三角形的斜边上的高为折痕,翻折和,使得平面平面.下列结论错误的是()A.B.是等边三角形C.三棱锥是正三棱锥D.平面平面学科网(北京)股份有限公司【答案】(1)C;(2)D.变式:(1)已知正三角形的中线与中位线相交于点,是绕旋转过程中的一个图形,则下列结论错误的是()A.动点在平面上的射影在线段上B.三棱锥的体积有最大值C.恒有平面平面D.异面直线与不可能互相垂直【答案】D(2)如图,在矩形中,,为的中点,将沿直线翻折成,若是线段的中点,则在翻折的过程中,下列命题正确的是()A.是定值B.的轨迹是一段圆弧C.平面D.存在某个位置,使得【答案】D例2.(1)已知矩形,,将沿矩形的对角线所在的直线经翻折,在翻折过程中()A.存在某个位置,使得直线与垂直B.存在某个位置,使得直线与垂直C.存在某个位置,使得直线与垂直D.对任意位置,三对直线“与”,“与”,“与”均不垂直(2)如图,在菱形中,,线段的中点分别为,现将学科网(北京)股份有限公司沿对角线翻折,则异面直线与所成角的取值范围是()A.B.C.D.【答案】(1)B;(2)C..变式:1.在正方形中,点分别是的中点,将沿所在的直线进行翻折,将沿所在的直线进行翻折,在翻折的过程中,()A.点与点在某一位置可能重合B.点与点的最大距离为C.直线与直线可能垂直D.直线与直线可能垂直【答案】D2.如图,在中,,,是斜边的中点,将沿直线翻折,若在翻折过程中存在某个位置,使得,则的取值范围是()A.B.C.D.【答案】A例3.(1)如图,在长方形中,,为线段上一动点,现将沿折起,使得点在面上的射影在直线上,当从运动到,则所形成的轨迹的长度是__________.学科网(北京)股份有限公司(2)如图,在长方形中,,,为的中点,为线段(端点除外)上一动点.现将沿折起,使平面平面.在平面内过点作,为垂足.设,则的取值范围是.【答案】(1);(2...