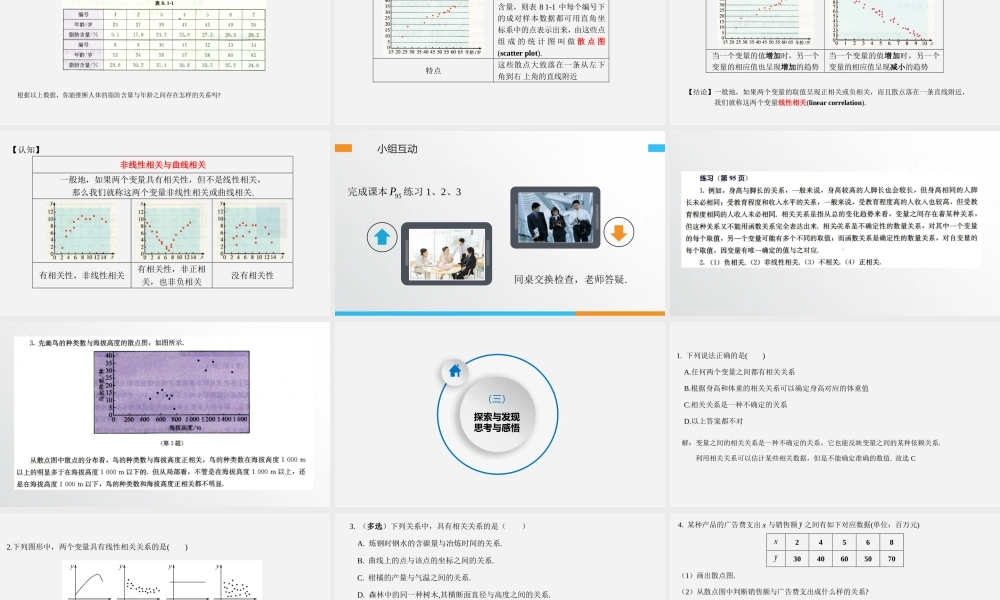
8.1.1变量的相关关系第八章成对数据的统计分析凯里一中尹洪January26,2025(一)创设情境揭示课题【背景】如果变量y是变量x的函数,那么由x就可以唯一确定y.然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度.例如,人的体重与身高存在关系,但由一个人的身高值并不能确定他的体重值.那么,该如何刻画这两个变量之间的关系呢?【情景一】子女身高y与父亲身高x之间的关系【情景二】商品销售收入y与广告支出x之间的关系【情景三】空气污染指数y与汽车保有量x之间的关系【情景四】粮食亩产量y与施肥量x之间的关系【问题】以上的变量关系如何描述?【研读与思考】阅读课本9395PP,与同桌或小组交流.(用时约3-5分钟)(二)阅读精要研讨新知【发现】一个人的体重与他的身高有关系,但身高并不是决定体重的唯一因素.例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素.像这样,两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系(correlation).以上的情景一、情景二、情景三与情景四中的变量关系都属于相关关系.【解读】在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表8.1-1所示,表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.根据以上数据,你能推断人体的脂防含量与年龄之间存在怎样的关系吗?【发现】散点图(scatterplot)--用图形展示成对样本数据的变化特征用横轴表示年龄,纵轴表示脂肪含量,则表81-1中每个编号下的成对样本数据都可用直角坐标系中的点表示出来,由这些点组成的统计图叫做散点图(scatterplot).特点这些散点大致落在一条从左下角到右上角的直线附近正相关与负相关正相关负相关当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势当一个变量的值增加时,另一个变量的相应值呈现减小的趋势【结论】一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关(linearcorrelation).【认知】非线性相关与曲线相关一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.有相关性,非线性相关有相关性,非正相关,也非负相关没有相关性小组互动完成课本95P练习1、2、3同桌交换检查,老师答疑.(三)探索与发现思考与感悟1.下列说法...