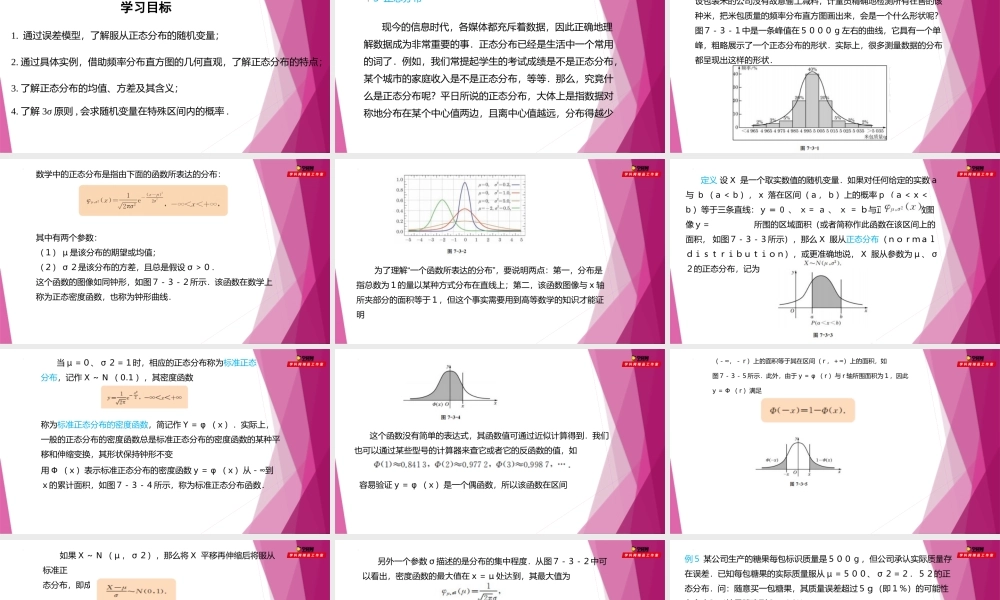
2022-2023学年高一数学同步精品课堂(沪教版2020选修第二册)第7章概率初步(续)7.3正态分布(第3课时)学习目标1.通过误差模型,了解服从正态分布的随机变量;2.通过具体实例,借助频率分布直方图的几何直观,了解正态分布的特点;3.了解正态分布的均值、方差及其含义;4.了解3σ原则,会求随机变量在特殊区间内的概率.3正态分布现今的信息时代,各媒体都充斥着数据,因此正确地理解数据成为非常重要的事.正态分布已经是生活中一个常用的词了.例如,我们常提起学生的考试成绩是不是正态分布,某个城市的家庭收入是不是正态分布,等等.那么,究竟什么是正态分布呢?平日所说的正态分布,大体上是指数据对称地分布在某个中心值两边,且离中心值越远,分布得越少一包米的外包装上标示的5000g,但实际上是有误差的.假设包装米的公司没有故意偷工减料,计量员精确地检测所有在售的该种米,把米包质量的频率分布直方图画出来,会是一个什么形状呢?图7-3-1中是一条峰值在5000g左右的曲线,它具有一个单峰,粗略展示了一个正态分布的形状.实际上,很多测量数据的分布都呈现出这样的形状.数学中的正态分布是指由下面的函数所表达的分布:其中有两个参数:(1)μ是该分布的期望或均值;(2)σ2是该分布的方差,且总是假设σ>0.这个函数的图像如同钟形,如图7-3-2所示.该函数在数学上称为正态密度函数,也称为钟形曲线.“”为了理解一个函数所表达的分布,要说明两点:第一,分布是指总数为1的量以某种方式分布在直线上;第二,该函数图像与x轴所夹部分的面积等于1,但这个事实需要用到高等数学的知识才能证明定义设X是一个取实数值的随机变量.如果对任何给定的实数a与b(a<b),x落在区间(a,b)上的概率p(a<x<b)等于三条直线:y=0、x=a、x=b与正态密度函数图像y=所围的区域面积(或者简称作此函数在该区间上的面积,如图7-3-3所示),那么X服从正态分布(normaldistribution),或更准确地说,X服从参数为μ、σ2的正态分布,记为当μ=0、σ2=1时,相应的正态分布称为标准正态分布,记作X~N(0.1),其密度函数称为标准正态分布的密度函数,简记作Y=φ(x).实际上,一般的正态分布的密度函数总是标准正态分布的密度函数的某种平移和伸缩变换,其形状保持钟形不变用Φ(x)表示标准正态分布的密度函数y=φ∞(x)从-到x的累计面积,如图7-3-4所示,称为标准正态...