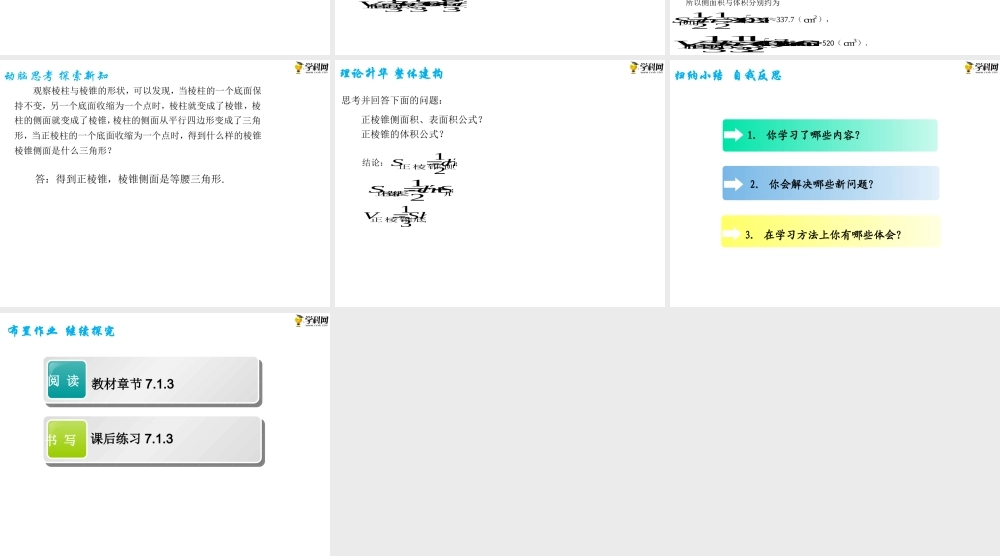
7.1.3棱锥第七章简单几何体创设情境兴趣导入观察图7−13所示的多面体,它们有什么共同点?可以发现,这些多面体都有一个面是多边形,其余各面是三角形,且这些三角形有一个公共点.我们称这样的多面体为棱锥.这个多边形称为棱锥的底面(简称底),其余各面称为棱锥的侧面;各侧面的公共点称为棱锥的顶点,如图7−13中所示的点P;相邻侧面的公共边称为棱锥的侧棱,如图7−13中所示的PA、PB、PC;顶点到底面的距离称为棱锥的高,如图7−13中所示的PO.动脑思考探索新知类似于棱柱,底面是三角形、四边形、……的棱锥分别叫做三棱锥、四棱锥、…….并分别记作棱锥P-ABC、棱锥P-ABCD等.底面是正多边形,顶点在底面内的投影是底面中心的棱锥称为其叫做正棱锥.正棱锥侧面三角形的高称为棱锥的斜高,如图7−14中的h.正棱锥有下列性质:(1)各侧棱的长相等,斜高相等,侧面都是全等的等腰三角形;(2)顶点到底面中心的连线垂直与底面,是正棱锥的高;(3)正棱锥的高、斜高与斜高在底面的投影组成一个直角三角形,正棱锥的高、侧棱与侧棱在底面的投影也组成一个直角三角形.动脑思考探索新知把棱锥的侧面沿一条侧棱展开在一个平面上所得的图形称为棱锥的侧面展开图,展开图的面积称为棱锥的侧面积,如图7−14所示.正棱锥的侧面展开图由各个等腰三角形组成,由此得到正棱锥的侧面积和表面积:全面积(表面积)计算公式分别为hcS21正棱锥侧12SchS正棱锥表底.其中,c表示正棱锥底面的周长,h是正棱锥的斜高,底S表示正棱锥的底面的面积.创设情境兴趣导入准备好同底等高的正三棱锥与正三棱柱形容器,将正三棱锥容器中装满沙子,然后倒入正三棱柱形状的容器中,发现:连续倒三次正好将正三棱柱容器装满.实验表明,对于同底等高的棱锥与棱柱,棱锥的体积是棱柱体积的三分之一.即hSV底正棱锥31.其中,底S表示正棱锥的底面的面积,h是正棱锥的高.巩固知识典型例题例3如图7−16所示,正四棱锥P-ABCD的底面边长为4cm,斜高为25cm,求这个正四棱锥的表面积和体积.解正四棱锥P-ABCD的底面边长为4cm,所以底面周长4416ccm(),底面积244=16)Scm底(,斜高=25PEcmcm。所以S表=2chS底=12×16×25+16=165+16(2cm).作PO垂直于底面ABCD,连接OE,在Rt△POE中,222222(25)216(),POPEOEcmPO=4cm,所以棱锥的高h即PO为4cm,因此正四棱锥体积31164164=)333VShcm正棱锥底(运用知识强化练习如图正三棱锥P-ABC中,点O是底面...