6.3.2 二项式系数的性质 课件-2022-2023学年高二下学期数学人教A版（2019）选择性必修第三册.pptxVIP免费

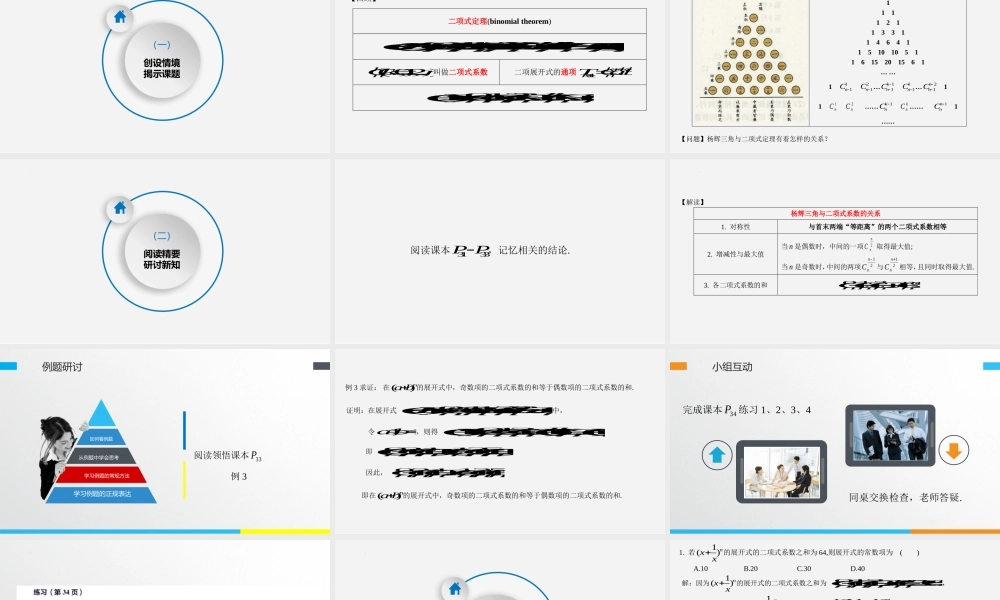
6.3.2二项式系数的性质第六章计数原理凯里一中尹洪January26,2025（一）创设情境揭示课题【回顾】二项式定理(binomialtheorem)011222*()......,nnnnknkknnnnnnnabCaCabCabCabCbnN(0,1,2,...,)knCkn叫做二项式系数二项展开式的通项1knkkknTCab0122(1)......nkknnnnnnnxCCxCxCxCx【情景】杨辉三角111121133114641151010511615201561……111nC21nC…11knC1knC…21nnC111nC2nC……1knCknC……1nnC1……【问题】杨辉三角与二项式定理有着怎样的关系？（二）阅读精要研讨新知阅读课本3133PP，记忆相关的结论.【解读】杨辉三角与二项式系数的关系1.对称性与首末两端“等距离”的两个二项式系数相等2.增减性与最大值当n是偶数时，中间的一项2nnC取得最大值;当n是奇数时，中间的两项12nnC与12nnC相等，且同时取得最大值.3.各二项式系数的和012...2nnnnnnCCCC例题研讨学习例题的正规表达学习例题的常规方法从例题中学会思考如何看例题阅读领悟课本33P例3例3求证：在()nab的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.证明：在展开式011222()...nnnnnnnnnnabCaCabCabCb中，令1,1ab，则得012(11)...(1)...(1)nkknnnnnnnCCCCC即024135(...)(...)0nnnnnnCCCCCC因此，024135......nnnnnnCCCCCC即在()nab的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.小组互动完成课本34P练习1、2、3、4同桌交换检查，老师答疑.（三）探索与发现思考与感悟1.若1()nxx的展开式的二项式系数之和为64,则展开式的常数项为()A.10B.20C.30D.40解：因为1()nxx的展开式的二项式系数之和为0126...2642nnnnnnCCCC，解得6n,所以61()xx的通项为662166kkkkkkTCxxCx令620k，则3k，所以常数项为3620C，故选B2.设2921101211(1)(21)(2)(2)...(2)xxaaxaxax,则01211...aaaa的值为()A.2B.2C.1D.1解：令1x,则原式化为2921101211(11)(21)(12)(12)...(12)aaaa所以01211...2aaaa，故选A.3.如果21()2nxx的展开式中只有第4项的二项式系数最大,那么展开式中的所有项的系数之和是()A.0B.256C.64D.164解：由题意知,只有第4项的二项式系数最大,所以6n,令1x,则展开式中的所...