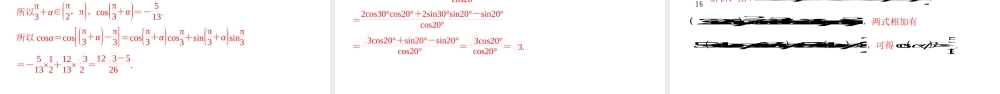5.5.1三角恒等变换第1课时两角差的余弦公式学习目标素养目标学科素养1.会用两点间距离公式推导出两角差的余弦公式;2.熟记两角差的余弦公式,并能灵活运用.1.直观想象2.数学运算自主学习推导:如图所示,设单位圆与x轴的正半轴相交于点A(1,0),以x轴非负半轴为始边作角α,β,α-β,它们的终边分别与单位圆相交于点P1、A1、P.思考:P1、A1、P点的坐标如何表示?线段AP和A1P1有什么关系?P1(cosα,sinα)、A1(cosβ,sinβ)、P(cos(α-β),sin(α-β))AP=A1P1自主学习两角差的余弦公式名称简单符号公式使用条件两角差的余弦C(α-β)cos(α-β)=cosαcosβ+sinαsinβα,β为任意角1.思考辨析(正确的画“√”,错误的画“×”)(1)cos(60°-30°)=cos60°-cos30°.()(2)对任意α,β∈R,cos(α-β)=cosαcosβ+sinαsinβ都成立.()(3)cos30°cos120°+sin30°sin120°=0.()(4)求cosα时,有时把角α看成角α+β与角β的差.()×小试牛刀√√√小试牛刀2.cos45°cos15°+sin45°sin15°等于()A.12B.32C.33D.33.已知sinθ=,cosθ=,则cos(θ-)=()A.B.C.D.B解析:原式=cos(45°-15°)=cos30°=32.B解析: sinθ=,cosθ=,∴cos(θ-)=cosθcos+sinθsin=cosθ+sinθ==.题型一给角求值例1计算:(1)cos(-15°);(2)cos15°cos105°+sin15°sin105°.经典例题解:解法一:原式=cos(30°-45°)=cos30°cos45°+sin30°sin45°=32×22+12×22=6+24.解法二:原式=cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30°=22×32+22×12=6+24.(2)原式=cos(15°-105°)=cos(-90°)=cos90°=0.总结利用公式C(α-β)求值的思路方法1.求非特殊角的余弦值时可将角转化为特殊角的差,正用公式直接求值.2.如果函数名称不满足公式特点,可利用诱导公式调整角和函数名称,构造公式的结构形式然后逆用公式求值.题型一给角求值经典例题跟踪训练1求下列各式的值:(1)cos75°cos15°-sin75°sin195°;(2).解:(1)cos75°cos15°-sin75°sin195°=cos75°cos15°+sin75°sin15°=cos(75°-15°)=cos60°=.(2)原式====cos15°=cos(60°-45°)=.题型一给角求值经典例题题型二给值求值例2已知α∈(0,),cos(α+)=,则cosα的值为________.经典例题解析:因α∈(0,),即<α+<,又cos(α+)=,则sin(α+)==,所以cosα=cos[(α+)-]=cos(α+)cos+sin(α+)sin=)=...