5.4 三角数的图象与性质(含3课时)-2022-2023学年高一数学教材配套教学精品课件（人教A版2019必修第一册).pptxVIP免费

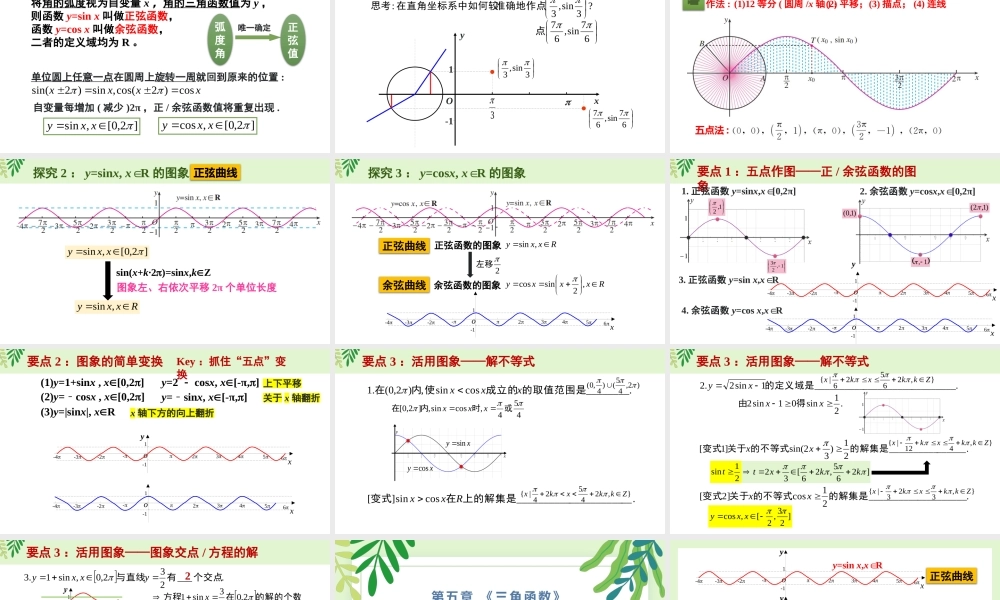
第五章《三角函数》5.4.1正弦函数、余弦函数的图象将角的弧度视为自变量x，角的三角函数值为y，则函数y=sinx叫做正弦函数，函数y=cosx叫做余弦函数，二者的定义域均为R。正弦函数、余弦函数的定义单位圆上任意一点在圆周上旋转一周就回到原来的位置:xxxxcos)2cos(,sin)2sin(]2,0[,sinxxy自变量每增加(减少)2π，正/余弦函数值将重复出现.]2,0[,cosxxy弧度角唯一确定正弦值1-1?3sin,3:准确地作点在直角坐标系中如何较思考3sin,3yO3x67sin,67点探究1：y=sinx,x[0,2π]∈的图象67sin,67探究1：y=sinx,x[0,2π]∈的图象作法:(1)12等分(圆周/x轴)；(2)平移；(3)描点；(4)连线五点法:正弦曲线sin(x+k·2)=sinx,kZ图象左、右依次平移2π个单位长度]2,0[,sinxxyRxxy,sin探究2：y=sinx,xR∈的图象探究3：y=cosx,xR∈的图象余弦函数的图象正弦函数的图象正弦曲线余弦曲线Rxxxy,2sincos2左移Rxxy,sinx6o--12345-2-3-41要点1：五点作图——正/余弦函数的图象1.正弦函数y=sinx,x[0,2π]∈2.余弦函数y=cosx,x[0,2π]∈1,231,2)1,0(1,)1,2(x6o--12345-2-3-41x6yo--12345-2-3-413.正弦函数y=sinx,xR∈4.余弦函数y=cosx,xR∈要点2：图象的简单变换(1)y=1+sinx,x[0,2](2)y=cos﹣x,x[0,2]y=sin﹣x,x[-π,]y=2－cosx,x[-π,](3)y=|sinx|,xR上下平移关于x轴翻折x轴下方的向上翻折上下平移x轴下方的向上翻折Key：抓住“五点”变换x6o--12345-2-3-41x6yo--12345-2-3-41要点3：活用图象——解不等式.________cossin,)2,0(.1的取值范围是成立的使内在xxx454,cossin,]2,0[或时内在xxxyxxysinxycos.______________________cossin][上的解集是在变式Rxx)2,45()4,0(},24524|{Zkkxkx要点3：活用图象——解不等式._____________________________1sin2.2的定义域是xy.21sin01sin2xx得由},26526|{Zkkxkx.____________________21cos]2[的解集是的不等式关于变式xx.________________21)32sin(]1[的解集是的不等式关于变式xx]265,26[32kkxt},412|{Zkkxkx...