5.3函数的应用（3）（用二分法求函数零点）-2020-2021学年高一数学新教材配套课件（沪教版2020）.pptxVIP免费

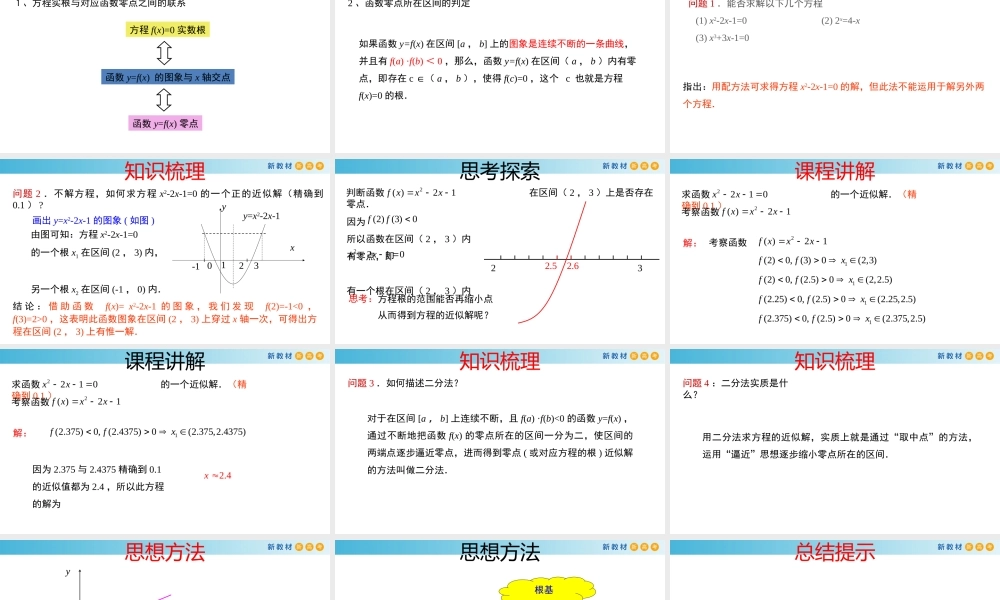
2020沪教版新教材第5章函数的概念、性质及应用5.3.3用二分法求函数零点复习回顾１、方程实根与对应函数零点之间的联系方程f(x)=0实数根函数y=f(x)的图象与x轴交点函数y=f(x)零点2、函数零点所在区间的判定如果函数y=f(x)在区间[a，b]上的图象是连续不断的一条曲线，并且有f(a)·f(b)＜0，那么，函数y=f(x)在区间（a，b）内有零点，即存在c∈（a，b），使得f(c)=0，这个c也就是方程f(x)=0的根．复习回顾知识梳理问题1．能否求解以下几个方程(1)x2-2x-1=0(2)2x=4-x(3)x3+3x-1=0指出：用配方法可求得方程x2-2x-1=0的解，但此法不能运用于解另外两个方程．问题2．不解方程，如何求方程x2-2x-1=0的一个正的近似解（精确到0.1）?画出y=x2-2x-1的图象(如图)xy1203y=x2-2x-1-1由图可知：方程x2-2x-1=0的一个根x1在区间(2，3)内，另一个根x2在区间(-1，0)内．结论：借助函数f(x)=x2-2x-1的图象，我们发现f(2)=-1<0，f(3)=2>0，这表明此函数图象在区间(2，3)上穿过x轴一次，可得出方程在区间(2，3)上有惟一解．知识梳理判断函数在区间（2，3）上是否存在零点．2()21fxxx因为所以函数在区间（2，3）内有零点，即有一个根在区间（2，3）内(2)(3)0ff2210xx232.62.5方程根的范围能否再缩小点从而得到方程的近似解呢？思考：思考探索课程讲解求函数的一个近似解．（精确到0.1）2210xx考察函数2()21fxxx解：考察函数2()21fxxx1(2)0,(3)0(2,3)ffx1(2)0,(2.5)0(2,2.5)ffx1(2.25)0,(2.5)0(2.25,2.5)ffx1(2.375)0,(2.5)0(2.375,2.5)ffx课程讲解求函数的一个近似解．（精确到0.1）2210xx考察函数2()21fxxx解：1(2.375)0,(2.4375)0(2.375,2.4375)ffx因为2.375与2.4375精确到0.1的近似值都为2.4，所以此方程的解为2.4x问题3．如何描述二分法？对于在区间[a，b]上连续不断，且f(a)·f(b)<0的函数y=f(x)，通过不断地把函数f(x)的零点所在的区间一分为二，使区间的两端点逐步逼近零点，进而得到零点(或对应方程的根)近似解的方法叫做二分法．知识梳理问题4：二分法实质是什么？用二分法求方程的近似解，实质上就是通过“取中点”的方法，运用“逼近”思想逐步缩小零点所在的区间．知识梳理xy0ab二分法思想方法对于在区间[a，b]上连续不断且f(a)·f(b)＜0的函数y=f(x)，通过不断地把函数f(x)的零点所在的区间一分为二，使区间的两个端点逼近零点，进而得到零点近似值．对于在①区间[a...