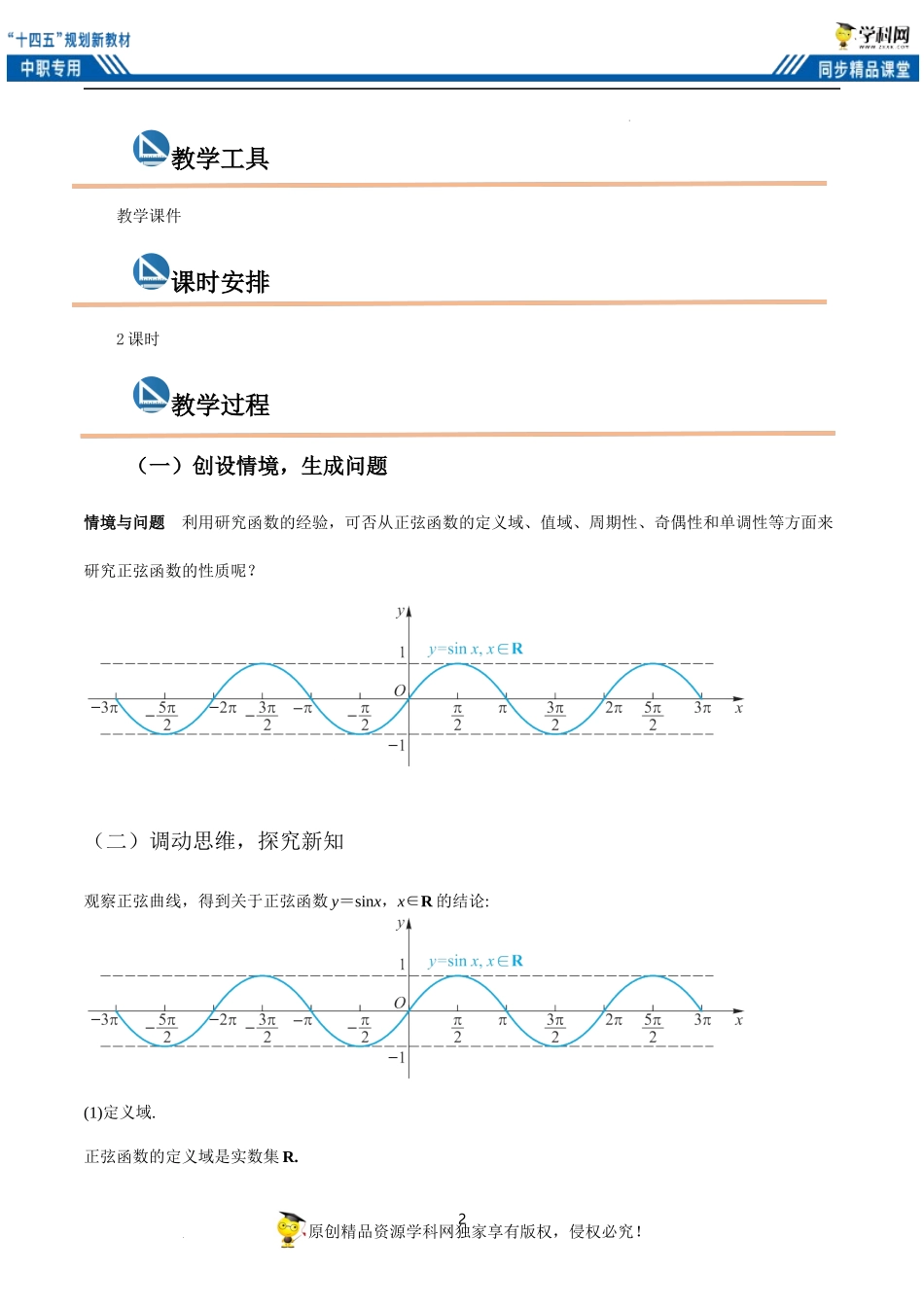
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司《4.6.2正弦函数的性质》教学设计学习目标学习重难点教材分析学生上节课学习了正弦函数的图像,本节课是在此基础上来学习正弦函数的性质,为学习余弦函数的图象和性质打好基础.学情分析学生在学习本节内容之前已学习了正弦函数的图像,具有一定的数学思想方法,但中职学生分析问题的能力不够深刻、严谨,所以本节内容的推导对学生有一定的难度.知识能力与素养理解正弦函数的图像和性质;(1)认识周期现象,以正弦函数为载体,理解周期函数;(2)通过对照学习研究,使学生体验类比的方法,从而培养数学思维能力.重点难点正弦函数的图像及性质周期性的理解.2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司教学工具教学课件课时安排2课时教学过程(一)创设情境,生成问题情境与问题利用研究函数的经验,可否从正弦函数的定义域、值域、周期性、奇偶性和单调性等方面来研究正弦函数的性质呢?(二)调动思维,探究新知观察正弦曲线,得到关于正弦函数y=sinx,x∈R的结论:(1)定义域.正弦函数的定义域是实数集R.3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司(2)值域.当时,y取最大值,当时,y取最小值,(3)周期性.正弦函数是周期为2π的周期函数.(4)奇偶性.由图像关于原点对称和诱导公式sin(−x)=−sinx可知,正弦函数是奇函数.(5)单调性.在每一个闭区间上都是增函数,函数值从-1增大到1;在每一个闭区间上都是减函数,函数值从1减小到-1.【设计意图】结合具体数值搭建思维台阶学生通过观察思考参与知识形成,感受发现的乐趣.(三)巩固知识,典例练习【典例1】求下列函数的最大值和最小值,并写出取得最大值、最小值时自变量x的集合.(1)解(1)由正弦函数的性质知,-1≤sinx≤1,所以故函数的最大值为,最小值为-4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司使函数取得最大值的集合就是使函数y=sinx,x∈R取得最大值的x的集合使函数取得最小值的x的集合,就是使函数y=sinx,x∈R取得最小值的x的集合(2)由正弦函数的性质知,-1≤sinx≤1,所以-2≤-2sinx≤2,-1≤1-2sinx≤3,即-1≤y≤3.故函数的最大值为3,最小值为-1.使函数y=1-2sinx,x∈R取得最大值的x的集合,就是使函数y=sinx,x∈R取得最小值的x的集合;使函数y=1-2sinx,x∈R取得最小值的x的集合,就是使函数y=sinx,x∈R取得最大值的x的集合....