22.1 比例线段（第3课时）.pptVIP免费

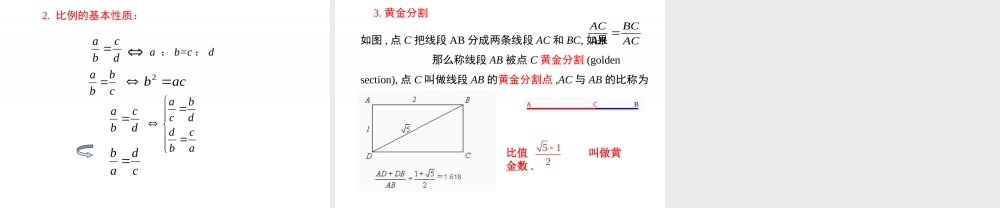
第3课时比例线段(3)问题1上节课学的比例线段的概念是怎样定义的？问题导入问题2比例线段要注意的方面有哪些？对于成比例线段我们有下面的结论：dcbadcba如果，那么ad＝bc．如果ad＝bc（a、b、c、d都不等于0），那么.你还可以得到其他的等比例式吗？讲授新课一、比例的基本性质dcbaddcbba例：证明：（1）如果，那么；acbd证明（1） 在等式两边同加上1，abcdbd∴．11acbd∴典例精讲∴ad＝bc，∴－ad＝－bc，在等式两边同加上ac，∴ac－ad＝ac－bc，∴a（c－d）＝（a－b）c，两边同除以（a－b）（c－d），dcbadccbaa（2）如果，那么acbdacabcd证明： ．∴合比性质：ddcbbadcbadcdcbaba等比性质：（b+d+···+m≠0）bamdbncamndcba.........总结归纳.yxyxyx的值，求已知43练一练问题1五角星是我们常见的图形.在图中,度量点C到点A,B的距离，?相等吗与ACBCABACACB如图,点C把线段AB分成两条线段AC和BC,如果那么称线段AB被点C黄金分割(goldensection),点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.ACBCABAC二、黄金分割问题2为什么叫做黄金分割?其一是满足黄金分割的图形具有和谐美;其二是黄金分割的应用价值不可估量,故冠以黄金二字.其实,黄金分割就是三条能构成比例线段的特殊线段AB,AC和BC.其中线段AC是线段AB和线段BC的比例中项,也可写成AC2=AB·BC.,5120.618.1ACBCABAC学习一元二次方程之后我们可以求得.,2ABCBCABACACBCABAC黄金分割线段那么点或如果确定黄金分割点的另一个方法•采用如下的方法也可以得到黄金分割点:如图任意作一条线段,用上述方法作出这条线段的黄金分割点.你能说说这种作法的道理吗?设AB是已知线段.在AB上作正方形ABCD.取AD的中点E,连接EB.延长DA至F,使EF=EB.以线段AF为边作正方形AFGH.点H就是AB的黄金分割点.ABCDEFGH拓展课堂练习.yxyxyx.的值，求已知43133=4472712xyk,xyk,xyxyk,xk,x.yyk,解：令(2)已知，线段MN被点C黄金分割,则MC2=MN·NC(MC＞NC）（）2.判断题(1)如图，点P是线段AB的黄金分割点，则（AP＜BP）（）.APBPABAPPABMNC课堂小结的比例中项；和叫做，那么如果cabcbba)1(.::,::,,,3cdbadcbadcba而不能写成是成比例线段，则，即成比例线段是有顺序的1.成比例线段像这样，对于四条线段a、b、c、d，如果其中两条线段的长度的...