22.1 比例线段（第3课时）.docVIP免费

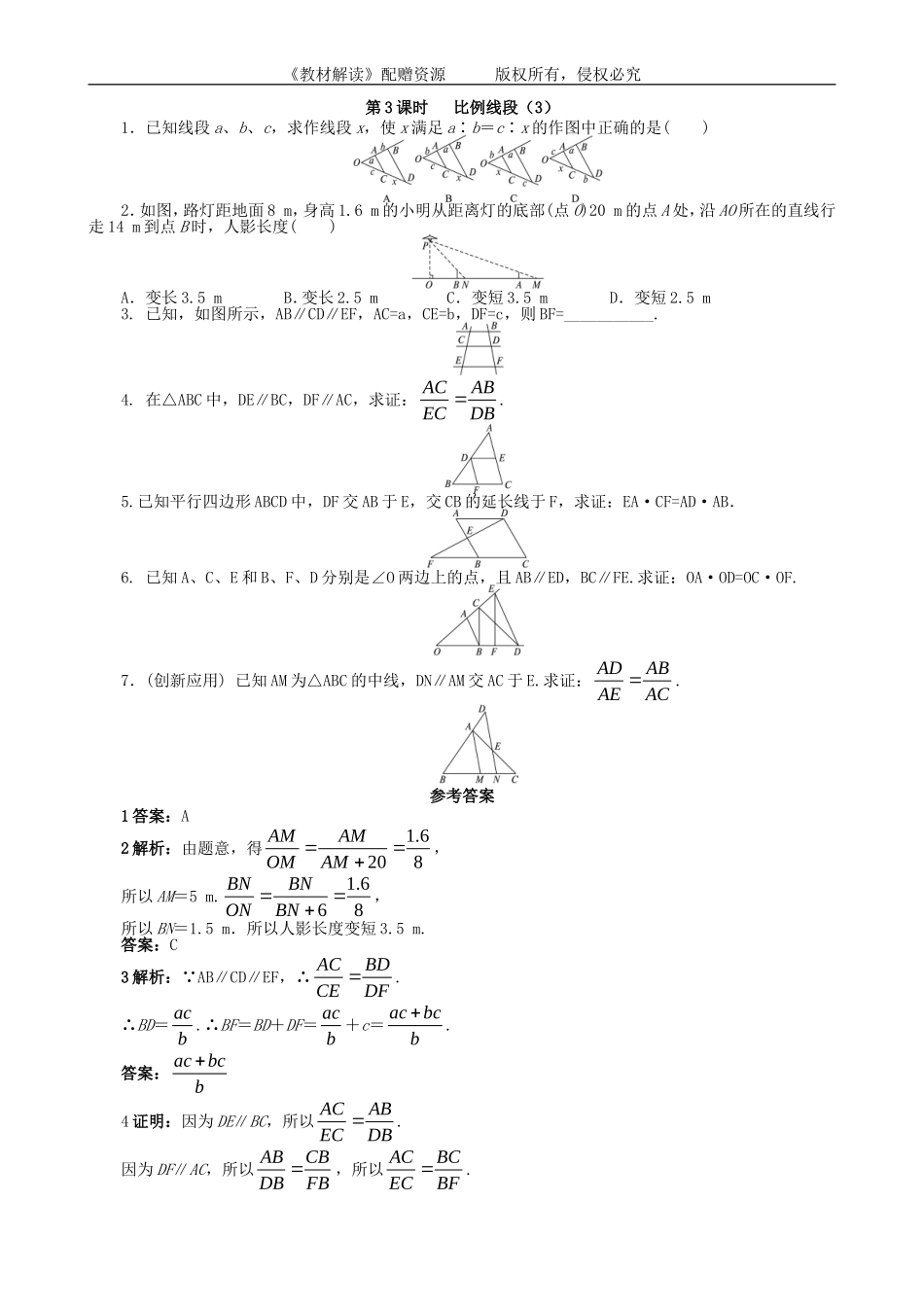
《教材解读》配赠资源版权所有，侵权必究第3课时比例线段（3）1．已知线段a、b、c，求作线段x，使x满足a∶b＝c∶x的作图中正确的是()2．如图，路灯距地面8m，身高1.6m的小明从距离灯的底部(点O)20m的点A处，沿AO所在的直线行走14m到点B时，人影长度()A．变长3.5mB．变长2.5mC．变短3.5mD．变短2.5m3.已知，如图所示，AB∥CD∥EF，AC=a，CE=b，DF=c，则BF=___________.4.在△ABC中，DE∥BC，DF∥AC，求证：ACABECDB.5.已知平行四边形ABCD中，DF交AB于E，交CB的延长线于F，求证：EA·CF=AD·AB．6.已知A、C、E和B、F、D分别是∠O两边上的点，且AB∥ED，BC∥FE.求证：OA·OD=OC·OF.7．(创新应用)已知AM为△ABC的中线，DN∥AM交AC于E.求证：ADABAEAC.参考答案1答案：A2解析：由题意，得1.6208AMAMOMAM，所以AM＝5m.1.668BNBNONBN，所以BN＝1.5m．所以人影长度变短3.5m.答案：C3解析：∵AB∥CD∥EF，∴ACBDCEDF.∴BD＝acb.∴BF＝BD＋DF＝acb＋c＝acbcb.答案：acbcb4证明：因为DE∥BC，所以ACABECDB.因为DF∥AC，所以ABCBDBFB，所以ACBCECBF.《教材解读》配赠资源版权所有，侵权必究5证明：∵四边形ABCD为平行四边形，∴AD∥FC，AB∥CD且BC=AD．∴EAEDABDF，EDBCADDFCFCF.∴EAADABCF.∴EA·CF=AD·AB．6证明：∵AB∥ED，∴OAOBOEOD.∴OA·OD=OB·OE.∵BC∥FE，∴OBOCOFOE.∴OB·OE=OF·OC．∴OA·OD=OC·OF.7证明：∵AM∥DN，∴ADMNABBM.∵AM为△ABC的中线，∴BM=CM.∴ADMNABMC.∵AM∥EN，∴MNAEMCAC.∴ADAEABAC，即ADABAEAC.