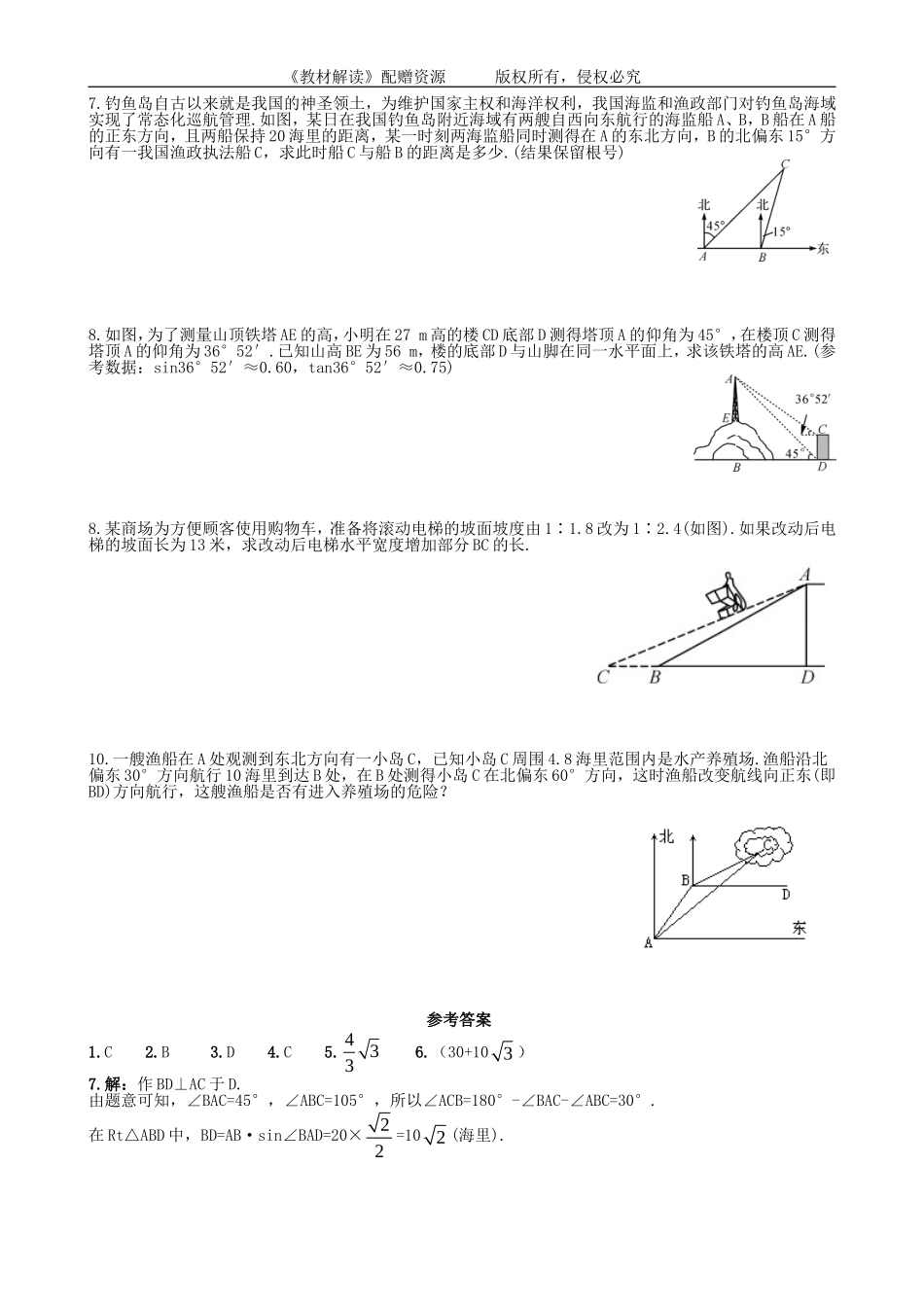
《教材解读》配赠资源版权所有,侵权必究第四章锐角三角函数4.4解直角三角形的应用基础导练1.如图,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为150米,且点A、D、B在同一直线上,建筑物A、B间的距离为()A.1503米B.1803米C.2003米D.2203米2.小强和小明去测量一座古塔的高度(如图),他们在离古塔60米的A处,用测角仪器得塔顶的仰角为30°,已知测角仪器高AD=1.5米,则古塔BE的高为()A.(203-1.5)米B.(203+1.5)米C.31.5D.28.53.由山顶A望地面C、D两点的俯角分别为450、300,若CD=100m,则山高AB等于()A.100mB.503mC.502mD.50(3+1)m4.某堤的横断面如图.堤高BC是5米,迎水斜坡AB的长时13米,那么斜坡AB的坡度是()A.1∶3B.1∶2.6C.1∶2.4D.1∶25.如图,坡角为30的斜坡上两树间的水平距离AC为2m,则两树间的坡面距离AB为6.如图,甲、乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为米.能力提升ABC《教材解读》配赠资源版权所有,侵权必究7.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)8.如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平面上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)8.某商场为方便顾客使用购物车,准备将滚动电梯的坡面坡度由1∶1.8改为1∶2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.10.一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?参考答案1.C2.B3.D4.C5.4336.(30+103)7.解:作BD⊥AC于D.由题意可知,∠BAC=45°,∠ABC=105°,所以∠ACB=180°-∠BAC-∠ABC=30°.在Rt△ABD中,BD=AB·sin∠BAD=20×22=102(海里).《教材解读》配赠资...