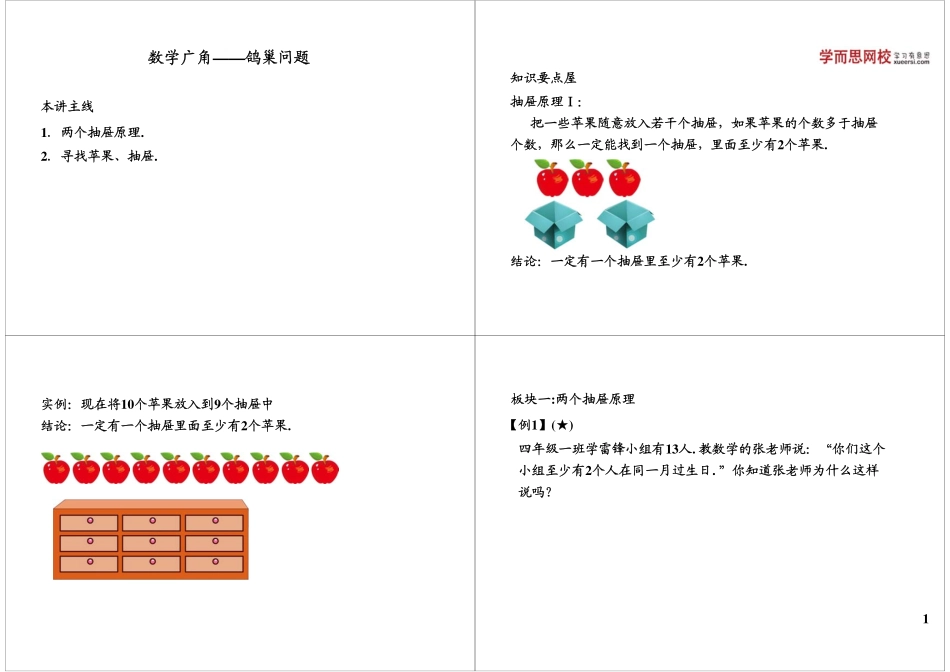
本讲主线1.两个抽屉原理.2.寻找苹果、抽屉.数学广角——鸽巢问题抽屉原理Ⅰ:把一些苹果随意放入若干个抽屉,如果苹果的个数多于抽屉个数,那么一定能找到一个抽屉,里面至少有2个苹果.知识要点屋结论:一定有一个抽屉里至少有2个苹果.实例:现在将10个苹果放入到9个抽屉中结论:一定有一个抽屉里面至少有2个苹果.【例1】(★)四年级一班学雷锋小组有13人.教数学的张老师说:“你们这个小组至少有2个人在同一月过生日.”你知道张老师为什么这样说吗?板块一:两个抽屉原理1抽屉原理Ⅰ1.苹果比抽屉多;2.结论:必定有一个抽屉里,至少有2个苹果.抽屉原理1.难点:找到抽屉和苹果.2.区分:苹果多,抽屉少.本题难点:抽屉:朋友数目的可能性.【例2】(★★)班上有28名小朋友,老师至少拿几本书,随意分给小朋友,才能保证至少有一个小朋友能得到不少于两本书?【例3】(★★★)五年级数学小组共有20名同学,他们在数学小组中都有一些朋友,请你说明:至少有两名同学,他们的朋友人数一样多.抽屉原理Ⅱ:把m个苹果放入n个抽屉中(m大于n),结果有两种可能:1.如果m÷n没有余数,那么就一定有抽屉至少放了“m÷n”个苹果;2.如果m÷n有余数,那么就一定有抽屉至少放了“m÷n的商再加1”个苹果.知识要点屋2抽屉原理Ⅱ:(实例)1.如果把8个苹果放到4个抽屉,那么一定有一个抽屉里至少放了个苹果.2.如果把9个苹果放到4个抽屉,那么一定有一个抽屉里至少放了个苹果.3.如果把14个苹果放到4个抽屉,那么一定有一个抽屉里至少放了个苹果.【例4】(★★★)⑴如果把98个苹果放到8个抽屉里,那么一定有抽屉至少放了___个苹果.⑵现在有10个抽屉,要想保证其中一个抽屉中至少有3个苹果,那么至少需要___个苹果.3【例5】(★★★☆)用红、蓝两种颜色将一个2×5方格图中的小方格随意涂色(见下图),每个小方格涂一种颜色.试说明必存在两列,它们的小方格中涂的颜色是完全相同的.板块二:寻找抽屉,苹果【例6】(★★★☆)17名同学参加一次考试,考试题是3道判断题(答案只有对错之分),每名同学都在答题纸上依次写上了3道题目的答案.试说明至少有3名同学的答案是一样的.知识大总结1.抽屉原理:将10个苹果放入到9个抽屉中,一定有一个抽屉里面至少有2个苹果.2.抽屉原理本质:“至少”,尽量平均分,结果是必有一个抽屉里的苹果不少于平均数(取整).3.难点:寻找苹果、抽屉.某件事情的可能性【今日讲题】例4,例5,例6_____________________________________________________...