PPT-第7章-异方差-计量经济学及Stata应用.pdfVIP免费

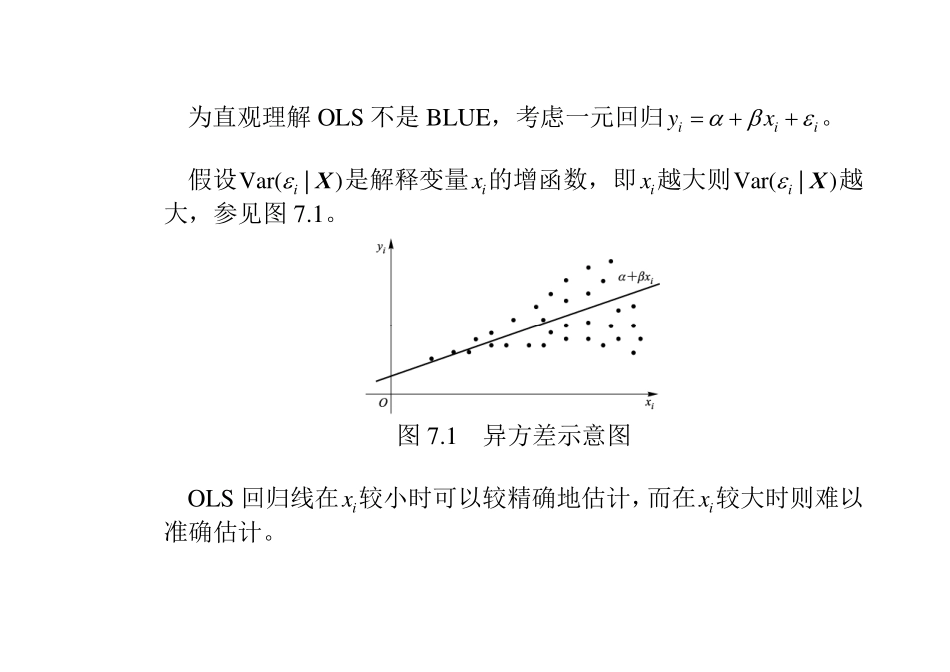
©陈强，2015年，《计量经济学及Stata应用》，高等教育出版社。第7章异方差现实的数据千奇百怪，常不符合古典模型的某些假定。从本章开始，逐步放松古典模型的各项假定。7.1异方差的后果“条件异方差”(conditionalheteroskedasticity)，简称“异方差”(heteroskedasticity)，是违背球型扰动项假设的一种情形，即条件方差Var(|)iX依赖于i，而不是常数2。在异方差的情况下：(1)OLS估计量依然无偏、一致且渐近正态。因为在证明这些性质时，并未用到“同方差”的假定。(2)OLS估计量方差ˆVar(|)βX的表达式不再是21()XX，因为2Var(|)εXI。使用普通标准误的t检验、F检验失效。(3)高斯-马尔可夫定理不再成立，OLS不再是BLUE(最佳线性无偏估计)。在异方差的情况下，本章介绍的“加权最小二乘法”才是BLUE。为直观理解OLS不是BLUE，考虑一元回归iiiyx。假设Var(|)iX是解释变量ix的增函数，即ix越大则Var(|)iX越大，参见图7.1。图7.1异方差示意图OLS回归线在ix较小时可以较精确地估计，而在ix较大时则难以准确估计。方差较大的数据包含的信息量较小，但OLS却对所有数据等量齐观进行处理；故异方差的存在使得OLS的效率降低。“加权最小二乘法”(WeightedLeastSquare，WLS)通过对不同数据所包含信息量的不同进行相应的处理以提高估计效率。比如，给予信息量大的数据更大的权重。计量经济学所指的“异方差”都是“条件异方差”，而非“无条件异方差”。比如，大样本理论要求样本数据为平稳过程，而平稳过程的方差不变。大样本理论是否已经假设同方差？关键要区分无条件方差(unconditionalvariance)与条件方差(conditionalvariance)。以一元回归模型iiiyx为例，假设,iixy为平稳过程，则iiiyx也是平稳过程，故其无条件方差2Var()i为常数，不随i而变。所有个体的条件方差函数1Var(|,,)inxx在函数形式上也完全相同；比如，21Var(|,,)inixxx。但此条件方差函数的具体取值却依赖于ix，故仍可存在条件异方差。比如，2111Var(|,,)nxxx，2212Var(|,,)nxxx，以此类推。7.2异方差的例子(1)考虑消费函数：iiicy(7.1)其中，ic为消费，iy为收入。富人的消费计划较有弹性，而穷人的消费多为必需品，很少变动。富人的消费支出更难测量，包含较多测量误差。Var(|)iiy可能随iy的上升而变大。(2)企业的投资、销售收入与利润：大型企业的商业活动可能动辄以亿元计，而小型...