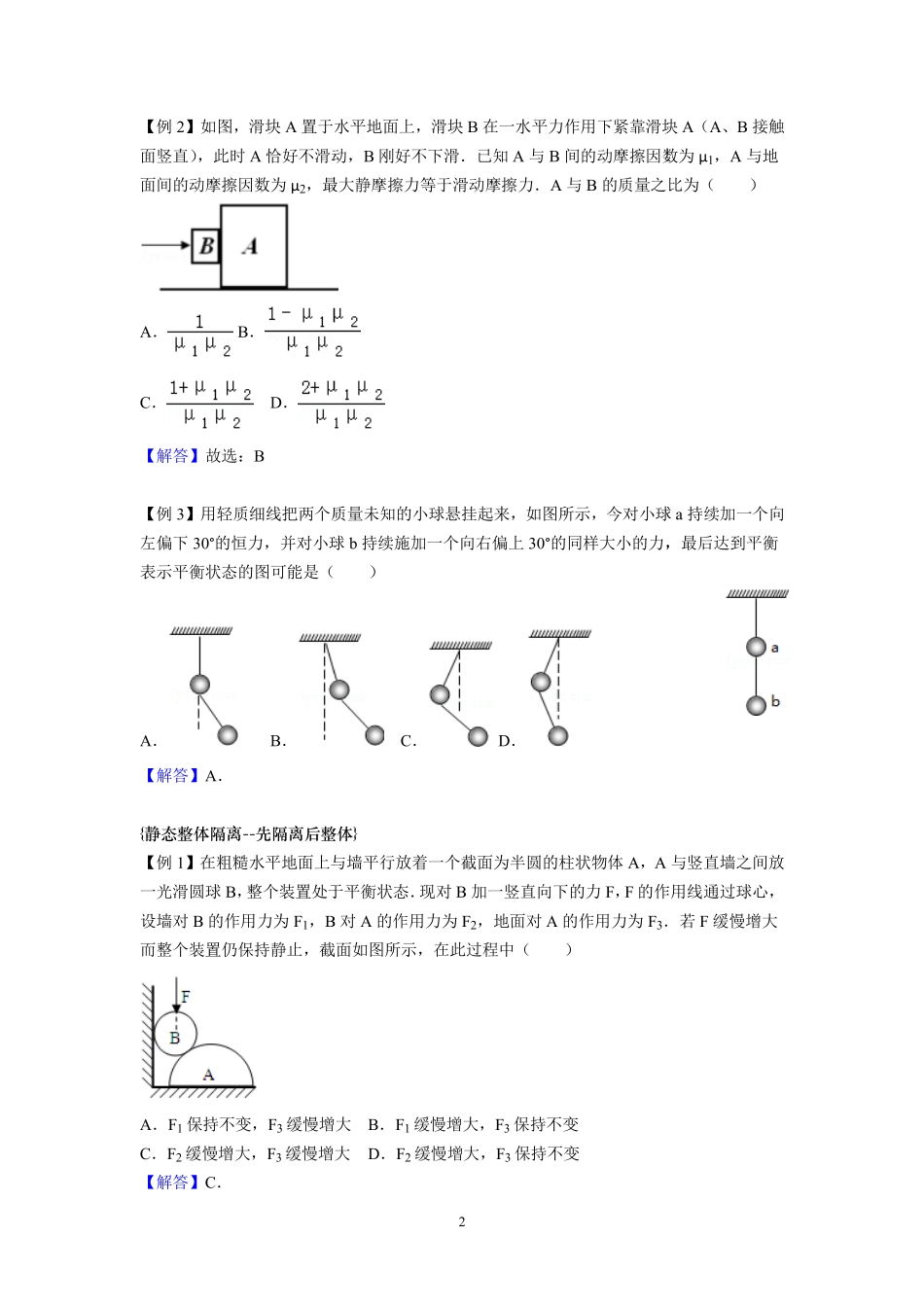
1第二章力的平衡§4拓展:整体隔离/临界问题【知识梳理】一、整体法与隔离法1、整体法:一般若讨论的问题不涉及系统内部的作用力时,可以以整个系统为研究对象列方程求解,这种方法称整体法.2、隔离法:若涉及系统中各物体间的相互作用,则应以系统某一部分为研究对象列方程求解,这种方法称隔离法.这样,便将物体间的内力转化为外力,从而体现其作用效果,使问题得以求解.在求解连接体问题时,隔离法与整体法相互依存,相互补充,交替使用,形成一个完整的统一体,分别列方程求解.二、临界问题1、某些物理现象在一定条件下才会发生,某些物理量在渐变过程中会发生突变,在即将发生突变时就出现临界问题.2、求解极值的方法可归纳为两种用物理规律求极值.如临界条件、边界条件等等.用数学方法求极值.如不等式、二次函数、三角函数和解三角形等等.【例题解析】{静态整体隔离--先整体后隔离}【例1】有一个直角支架AOB,AO水平放置,表面粗糙,OB竖直向下,表面光滑,AO上套有小环P,OB上套有小环Q,两环质量均为m,两环间由一根质量可忽略、不可伸展的细绳相连,并在某一位置平衡(如图),现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力N和细绳上的拉力T的变化情况是(B)A.N不变,T变大B.N不变,T变小C.N变大,T变大D.N变大,T变小【例2】如图,滑块A置于水平地面上面竖直),此时A恰好不滑动面间的动摩擦因数为μ2,最大静摩擦力等于滑动摩擦力A.B.C.D.【解答】故选:B【例3】用轻质细线把两个质量未知的小球悬挂起来左偏下30°的恒力,并对小球表示平衡状态的图可能是(A.B.【解答】A.{静态整体隔离--先隔离后整体【例1】在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体一光滑圆球B,整个装置处于平衡状态设墙对B的作用力为F1,B而整个装置仍保持静止,截面如图所示A.F1保持不变,F3缓慢增大C.F2缓慢增大,F3缓慢增大【解答】C.2置于水平地面上,滑块B在一水平力作用下紧靠滑块恰好不滑动,B刚好不下滑.已知A与B间的动摩擦因数为最大静摩擦力等于滑动摩擦力.A与B的质量之比为用轻质细线把两个质量未知的小球悬挂起来,如图所示,今对小球并对小球b持续施加一个向右偏上30°的同样大小的力,()C.D.先隔离后整体}在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A整个装置处于平衡状态.现对B加一竖直向下的力F,F的作用线通过球心B对A...