2 二重积分的计算-1.pptVIP免费

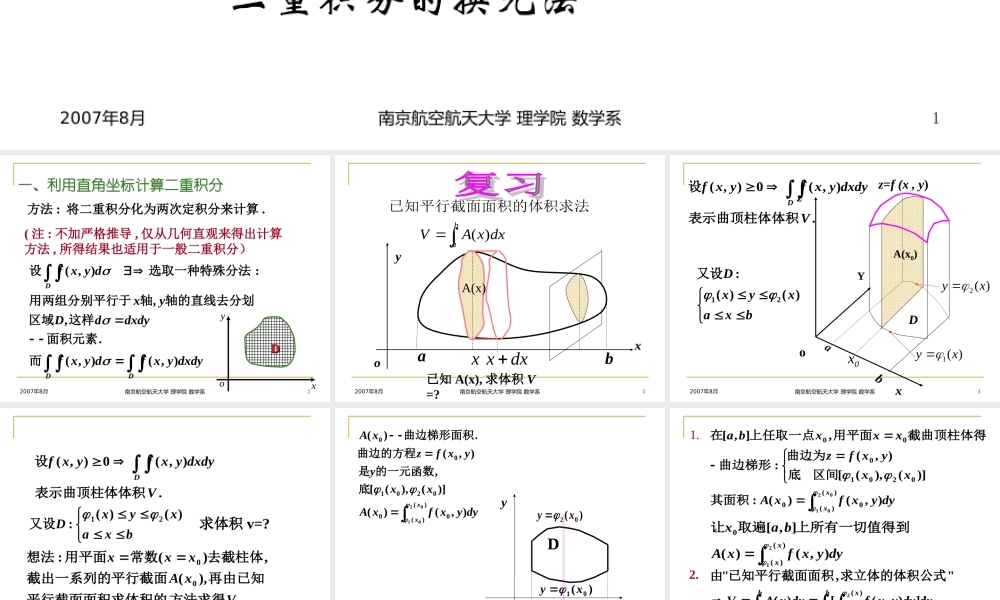
20078年月南京航空航天大学理学院数学系1二重积分的计算直角坐标系下二重积分的计算极坐标系下二重积分的计算二重积分的换元法20078年月南京航空航天大学理学院数学系2方法:将二重积分化为两次定积分来计算.(注:不加严格推导,仅从几何直观来得出计算方法,所得结果也适用于一般二重积分）一、利用直角坐标计算二重积分DDDdxdyyxfdyxfdxdydDyxdyxf),(),(.,,:),(而面积元素这样区域轴的直线去分划轴用两组分别平行于选取一种特殊分法设xyoDD20078年月南京航空航天大学理学院数学系3dxxbxyoaxA(x)已知A(x),求体积V=?badxxAV)(积求法已知平行截面面积的体20078年月南京航空航天大学理学院数学系4z=f(x,y)x0xzoYDabA(x0))(1xy)(2xy.),(0),(VdxdyyxfyxfD表示曲顶柱体体积设bxaxyxD)()(:21又设20078年月南京航空航天大学理学院数学系5.),(0),(VdxdyyxfyxfD表示曲顶柱体体积设bxaxyxD)()(:21又设求体积v=?VxAxxx方法求得平行截面面积求体积的再由已知截出一系列的平行截面去截柱体常数用平面想法),(,)(:00?)(0xA关键求20078年月南京航空航天大学理学院数学系6abD)(01xy)(02xyx0dyyxfxAxxyyxfzxAxx),()()](),([,),(.)()()(000201000201底的一元函数是曲边的方程曲边梯形面积xyo20078年月南京航空航天大学理学院数学系7dyyxfxAxxyxfzxxxbaxx),()(:)](),([),(:,],[)()(0002010000201其面积区间底曲边为曲边梯形截曲顶柱体得用平面上任取一点在)1(),(]),([)(",")()()()(2121baxxbaxxbadyyxfdxdxdyyxfdxxAV记求立体的体积公式已知平行截面面积由dyyxfxAbaxxx),()(],[)()(021上所有一切值得到取遍让1.2.20078年月南京航空航天大学理学院数学系8!0),()1(的限制可去掉中公式yxf如果积分区域为：,bxa).()(21xyx其中函数、在区间上连续.)(1x)(2x],[ba［X－型］)(2xyabD)(1xyDba)(2xy)(1xy.)1(),(),()()(21Dbaxxdyyxfdxdyxf注20078年月南京航空航天大学理学院数学系9)2(.),(),()()(21Ddcyydxyxfdydyxf如果积分区域为：,dyc).()(21yxy［Y－型］)(2yx)(1yxDcdcd)(2yx)(1yxD20078年月南京航空航天大学理学院数学系10X型区域的特点：穿过区域且平行于y轴的直线与区域边界相...