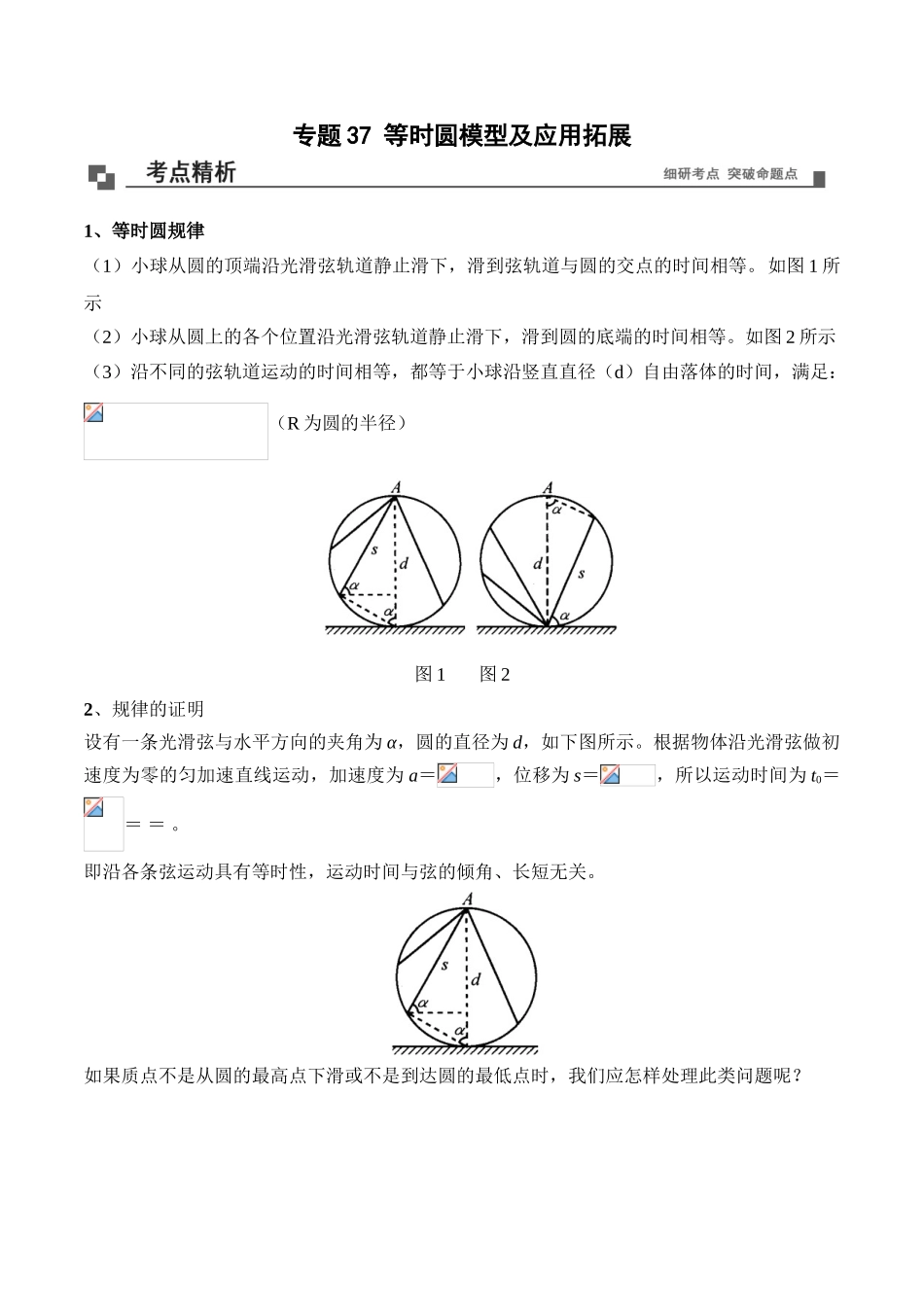
专题37等时圆模型及应用拓展1、等时圆规律(1)小球从圆的顶端沿光滑弦轨道静止滑下,滑到弦轨道与圆的交点的时间相等。如图1所示(2)小球从圆上的各个位置沿光滑弦轨道静止滑下,滑到圆的底端的时间相等。如图2所示(3)沿不同的弦轨道运动的时间相等,都等于小球沿竖直直径(d)自由落体的时间,满足:(R为圆的半径)图1图22、规律的证明设有一条光滑弦与水平方向的夹角为α,圆的直径为d,如下图所示。根据物体沿光滑弦做初速度为零的匀加速直线运动,加速度为a=,位移为s=,所以运动时间为t0===。即沿各条弦运动具有等时性,运动时间与弦的倾角、长短无关。如果质点不是从圆的最高点下滑或不是到达圆的最低点时,我们应怎样处理此类问题呢?图3图4[例题]如图3所示,AB、AC、AD是竖直面内三根固定的光滑细杆,A、B、C、D位于同一圆周上,O点为圆周的圆心,A点不是圆的最高点,每根杆上都套着一个光滑小滑环(图中未画出),三个滑环分别从A处从静止开始释放,用依次表示滑环到达B、C、D所用的时间,则三个时间的关系?解析:A不在圆的最高点,前面的结论直接用是不行的。可以采用如下的方法解决:如图4所示,过点A作竖直线交AB的垂直平分线于点O,以O1为圆心、O1A为半径画圆交AB于B、分别交AC、AD的延长线于C1、D1。r.在圆ABC1D1中用前面的结论可知,所以t1>t2。不可以根据CC1t3。一、单选题1.(2019·泉州第十六中学高三月考)如右图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点.竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心.已知在同一时刻a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点;c球由C点自由下落到M点.则()A.a球最先到达M点B.b球最后到达M点C.c球最后到达M点D.b球和c球都可能最先到达M点【答案】B【解析】设圆轨道半径为R,a小球做匀加速直线运动,加速度设为a1=gsin45°=,设时间为t1,由运动学分式可得联立可得t1=同理可求得B的加速度大小,设滑到低端时间为t2,由运动学公式可求得联立可得:t2=C球做自由落体运动,设运动时间为t3,由运动学公式可得比较以上数据可知C最先落到M点,A次之,B最后落在M点。2.(2017·江西高安中学高三月考)如图所示,在竖直平面内建立直角坐标系xOy,该平面内...