数学模型-第03章(第五版).pptxVIP免费

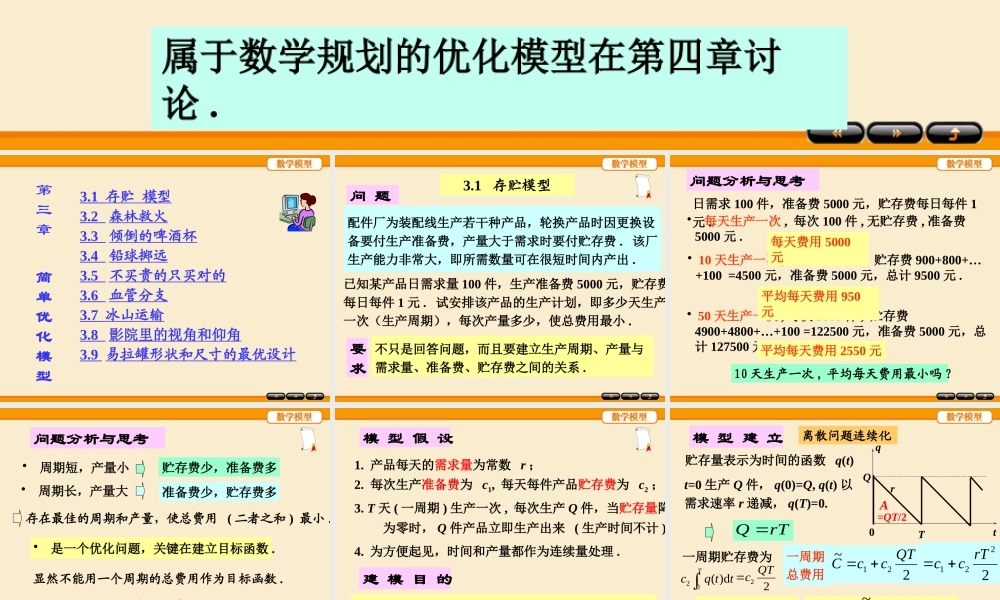
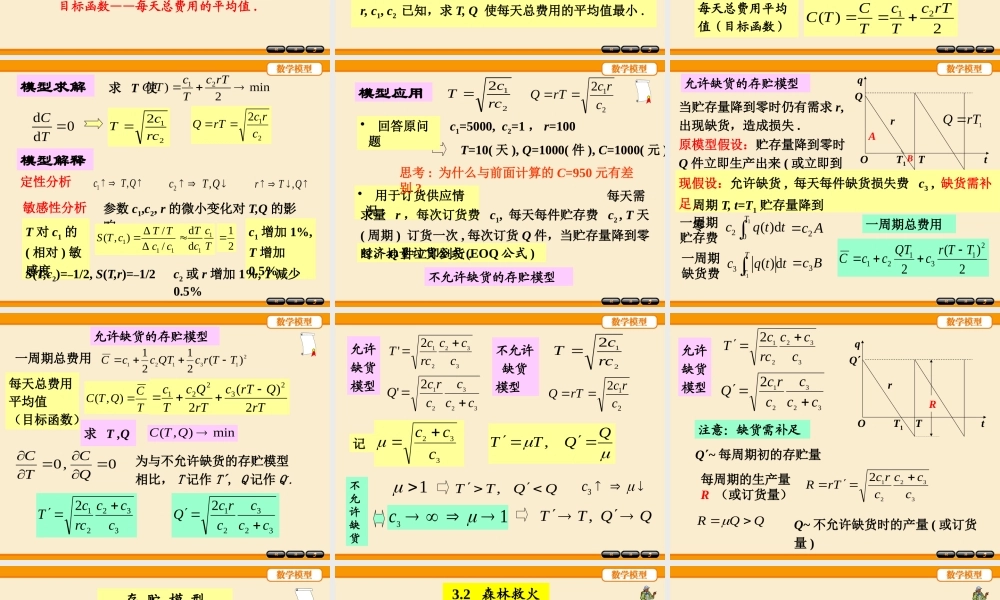
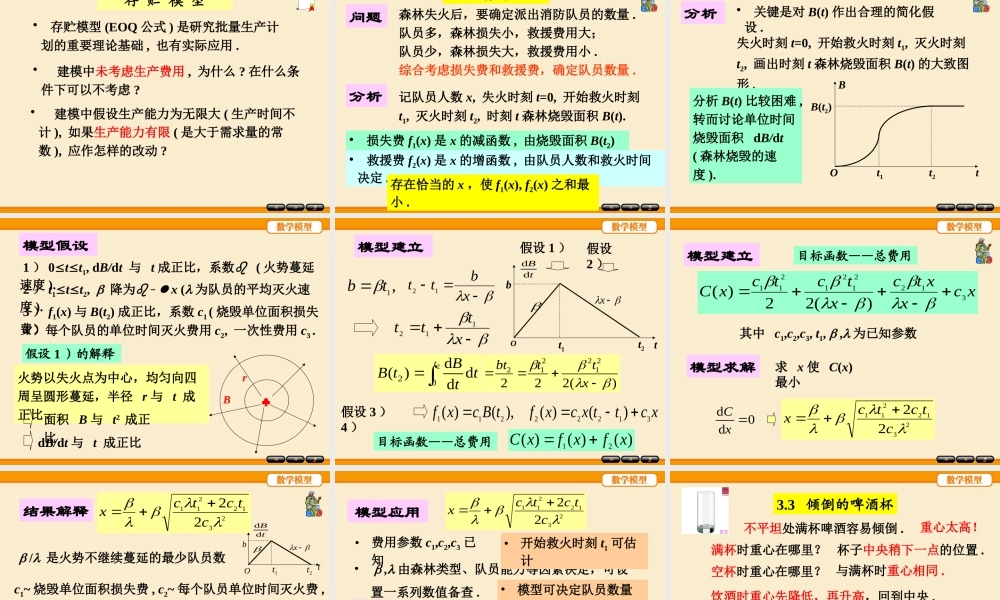
第三章简单优化模型优化——工程技术、经济管理、科学研究中的常见问题.用数学建模方法解决优化问题的过程简单优化模型归结为函数极值问题，用微分法求解.材料强度最大运输费用最低利润最高风险最小优化目标与决策模型假设与建立数学求解与分析属于数学规划的优化模型在第四章讨论.3.1存贮模型3.2森林救火3.3倾倒的啤酒杯3.4铅球掷远3.5不买贵的只买对的3.6血管分支3.7冰山运输3.8影院里的视角和仰角3.9易拉罐形状和尺寸的最优设计第三章简单优化模型3.1存贮模型问题配件厂为装配线生产若干种产品，轮换产品时因更换设备要付生产准备费，产量大于需求时要付贮存费.该厂生产能力非常大，即所需数量可在很短时间内产出.已知某产品日需求量100件，生产准备费5000元，贮存费每日每件1元.试安排该产品的生产计划，即多少天生产一次（生产周期），每次产量多少，使总费用最小.要求不只是回答问题，而且要建立生产周期、产量与需求量、准备费、贮存费之间的关系.问题分析与思考•每天生产一次,每次100件,无贮存费,准备费5000元.日需求100件，准备费5000元，贮存费每日每件1元.•10天生产一次,每次1000件，贮存费900+800+…+100=4500元，准备费5000元，总计9500元.•50天生产一次,每次5000件,贮存费4900+4800+…+100=122500元，准备费5000元，总计127500元.平均每天费用950元平均每天费用2550元10天生产一次,平均每天费用最小吗?每天费用5000元•是一个优化问题，关键在建立目标函数.显然不能用一个周期的总费用作为目标函数.目标函数——每天总费用的平均值.•周期短，产量小•周期长，产量大问题分析与思考贮存费少，准备费多准备费少，贮存费多存在最佳的周期和产量，使总费用(二者之和)最小.模型假设1.产品每天的需求量为常数r；2.每次生产准备费为c1,每天每件产品贮存费为c2；3.T天(一周期)生产一次,每次生产Q件，当贮存量降为零时，Q件产品立即生产出来(生产时间不计)建模目的r,c1,c2已知，求T,Q使每天总费用的平均值最小.4.为方便起见，时间和产量都作为连续量处理.模型建立0tq贮存量表示为时间的函数q(t)TQrt=0生产Q件，q(0)=Q,q(t)以需求速率r递减，q(T)=0.一周期总费用2~21QTccC每天总费用平均值（目标函数）2~)(21rTcTcTCTC离散问题连续化20()dTcqtt一周期贮存费为A2221rTccrTQ=QT/222QTc模型求解min2)(21rTcTcTC求T使d0dCT212crcrTQ212rccT模型解释QTc,1QTc,2QTr,定性分析敏感性分析参...