2017-2018学年湘教版数学选修2-2配套课件：4-1-2问题探索——求作抛物线的切线 -数学备课大师【全免费】.pptVIP免费

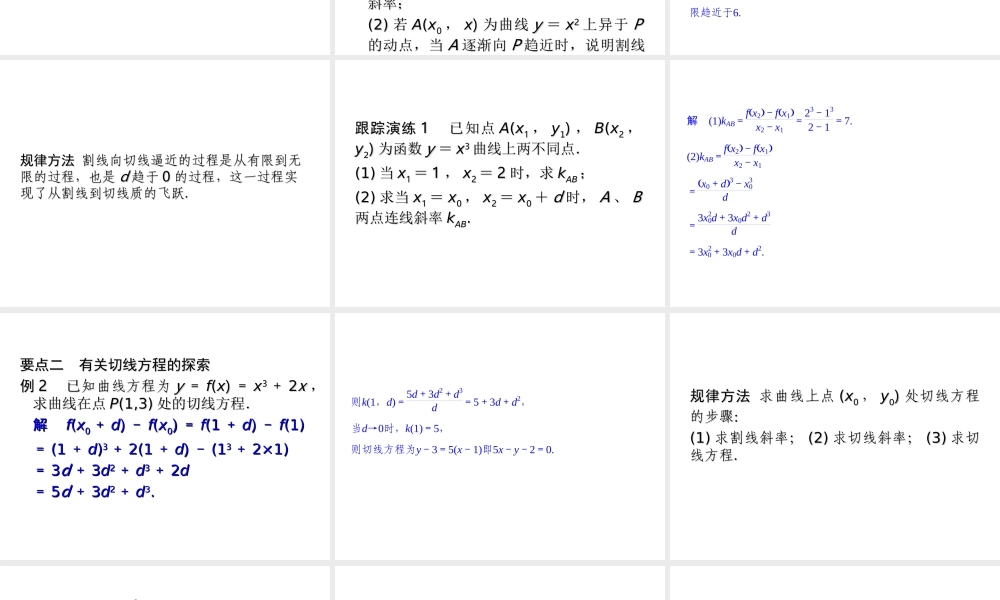
高中数学·选修2-2·湘教版4．1.2问题探索——求作抛物线的切线[[学习目标学习目标]]理理解并掌握如何求抛物线的切线．解并掌握如何求抛物线的切线．[知识链接]1．设函数y＝f(x)，当自变量x由x0改变到x0＋d时，函数的改变量Δy为________．答案f(x0＋d)－f(x0)2．函数y＝x2在x＝1处的切线斜率k＝________.答案ΔyΔx＝1＋Δx2－12Δx＝2＋Δx→2(Δx→0)．[预习导引]求曲线上点P处切线斜率的方法设P(u，f(u))是函数y＝f(x)的曲线上的任一点，则求点P处切线斜率的方法是：(1)在曲线上取不同于P的点Q(u＋d，f(u＋d))，计算直线PQ的斜率k(u，d)＝fu＋d－fud.(2)(2)在所求得的在所求得的PQPQ的斜率的表达式的斜率的表达式kk((uu，，dd))中，中，让让dd趋于趋于00，如果，如果kk((uu，，dd))趋于趋于的数值的数值kk((uu))，则，则就是曲线在就是曲线在PP处的切线斜率处的切线斜率..确定k(u)要点一有关曲线的割线斜率的探索要点一有关曲线的割线斜率的探索例例11点点PP(3,9)(3,9)为抛物线为抛物线yy＝＝xx22上的一点，上的一点，AA11(1,1)(1,1)，，AA22(2,4)(2,4)，，AA44(4,16)(4,16)，，AA55(5,25)(5,25)为抛物线上另外四点．为抛物线上另外四点．(1)(1)分别求割线分别求割线PAPA11，，PAPA22，，PAPA44，，PAPA55的的斜率；斜率；(2)(2)若若AA((xx00，，xx))为曲线为曲线yy＝＝xx22上异于上异于PP的动点，当的动点，当AA逐渐向逐渐向PP趋近时，说明割线趋近时，说明割线解(1)kPA1＝1－91－3＝4，kPA2＝4－92－3＝5，kPA4＝16－94－3＝7，kPA5＝25－95－3＝162＝8.(2)当A沿曲线趋近于P点时，x0的值趋近于3，不妨设x0＝3＋d(d≠0)，当x0→3时，d→0，则kPA＝x20－9x0－3＝x0＋3＝(3＋d)＋3＝6＋d，当d→0时，kPA→6，表明随A点无限趋近于P，割线PA的斜率无限趋近于6.规律方法规律方法割线向切线逼近的过程是从有限到无割线向切线逼近的过程是从有限到无限的过程，也是限的过程，也是dd趋于趋于00的过程，这一过程实的过程，这一过程实现了从割线到切线质的飞跃．现了从割线到切线质的飞跃．跟踪演练跟踪演练11已已知点知点AA((xx11，，yy11))，，BB((xx22，，yy22))为函数为函数yy＝＝xx33曲线上两不同点．曲线上两不同点．(1)(1)当当xx11＝＝11，，xx22＝＝22时，求时，求kkABAB；；(2)(2)求当求当xx11＝＝xx00，，xx22＝＝xx00＋＋dd时，时，AA、、BB两点连线斜率两点连线斜率kkABAB..解(1)kAB＝fx2－fx1x2－x1＝23－132－1＝7.(2...