湘教版选修1-1：2.2.1《双曲线的定义和标准方程》课件（3）.pptVIP免费

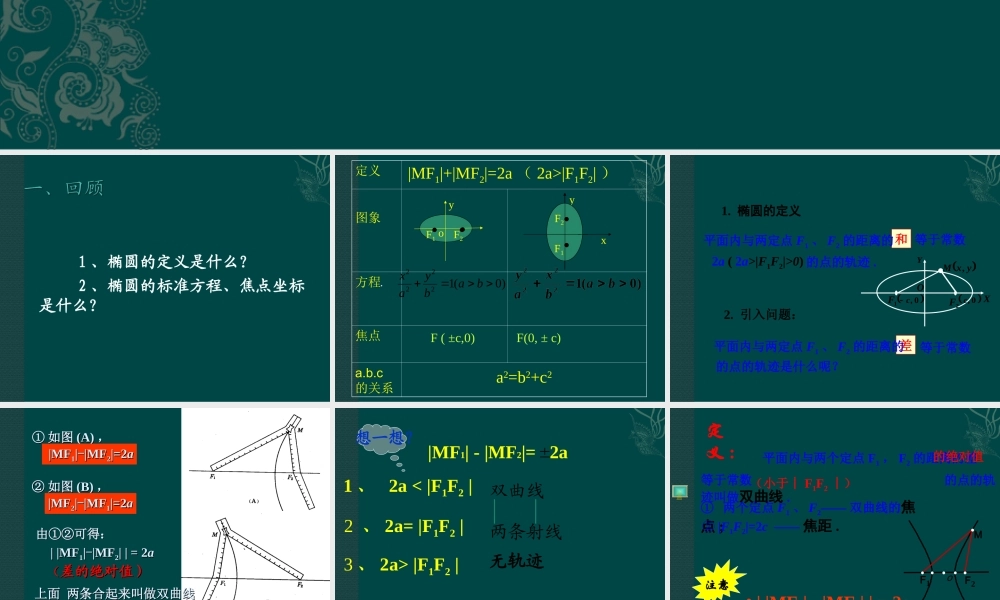
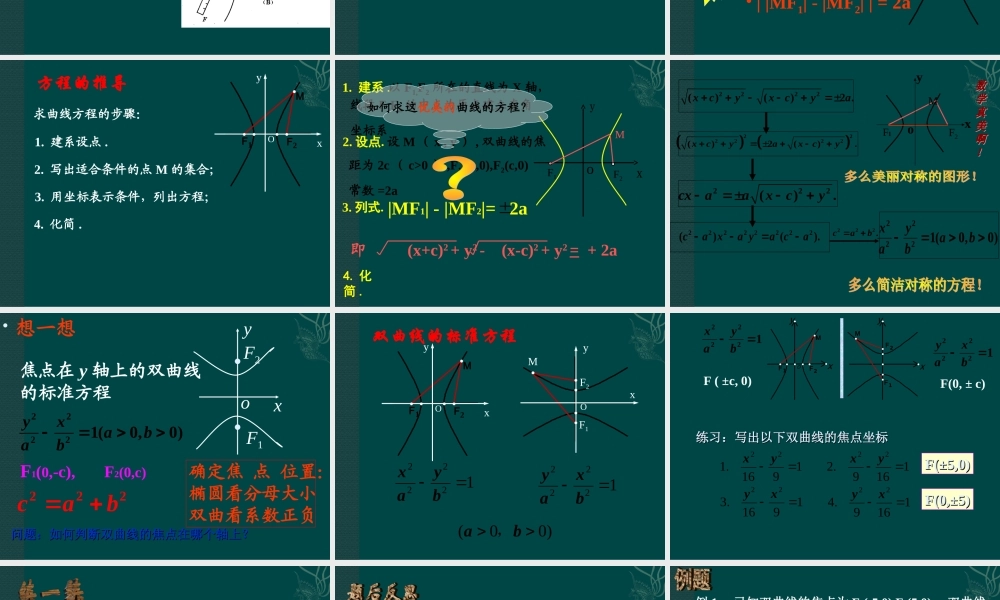
1、椭圆的定义是什么？2、椭圆的标准方程、焦点坐标是什么？定义图象方程焦点a.b.c的关系y·oxF1F2··yoF1F2··|MF1|+|MF2|=2a（2a>|F1F2|）a2=b2+c2F(±c,0)F(0,±c)oF1F2···)0(12222babyax1.椭圆的定义和等于常数2a(2a>|F1F2|>0)的点的轨迹.平面内与两定点F1、F2的距离的1F2F0,c0,cXYOyxM,2.引入问题：差等于常数的点的轨迹是什么呢？平面内与两定点F1、F2的距离的①①如图如图(A)(A)，，|MF|MF11||--|MF|MF22|=2|=2aa②②如图如图(B)(B)，，|MF|MF22||--|MF|MF11|=2|=2aa上面两条合起来叫做双曲线上面两条合起来叫做双曲线由①②可得：由①②可得：||MF||MF11||--|MF|MF22||=2||=2aa（（差的绝对值）差的绝对值）双曲线两条射线1、2a<|F1F2|2、2a=|F1F2|3、2a>|F1F2|无轨迹|MF1|-|MF2|=2a想一想？①两个定点F1、F2——双曲线的焦点;②|F1F2|=2c——焦距.oF2F1M平面内与两个定点F1，F2的距离的差等于常数的点的轨迹叫做双曲线.动画的绝对值（小于︱F1F2︱）注意定义:•||MF1|-|MF2||=2a1.建系设点.F2F1MxOy2.写出适合条件的点M的集合；3.用坐标表示条件，列出方程；4.化简.求曲线方程的步骤：方程的推导xyo设M（x,y）,双曲线的焦距为2c（c>0）,F1(-c,0),F2(c,0)常数=2aF1F2M即(x+c)2+y2-(x-c)2+y2=+2a_以F1,F2所在的直线为X轴，线段F1F2的中点为原点建立直角坐标系1.建系.2.设点．3.列式．|MF1|-|MF2|=2a如何求这优美的曲线的方程？4.化简.2222()()2.xcyxcya222222()2().xcyaxcy222().cxaaxcy22222222()().caxayacaoF2FMyx1222.cab22221(0,0)xyababF1F2yxo焦点在y轴上的双曲线的标准方程想一想F1(0,-c),F2(0,c)22221(0,0)yxabab222cab确定焦点位置：椭圆看分母大小双曲看系数正负问题：如何判断双曲线的焦点在哪个轴上？问题：如何判断双曲线的焦点在哪个轴上？12222byax12222bxayF2F1MxOyOMF2F1xy)00(ba，双曲线的标准方程F(±c,0)12222byax12222bxayyxoF2F1MxyF2F1MF(0,±c)练习：写出以下双曲线的焦点坐标练习：写出以下双曲线的焦点坐标1916.122yx1916.322xy1169.222yx1169.422xyF(±5,0)F(±5,0)F(0,±5)F(0,±5)判断下列方程是否表示双曲线？若是，求出及焦点坐标。cba,,2222222211214222314(0,0)42xyxyxynxmymnmn答案：12,2,6(6,0).(6,...