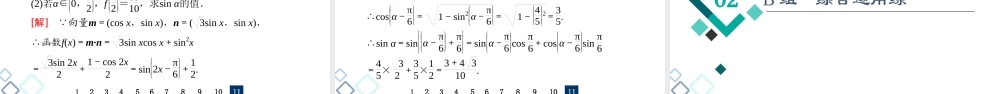课后限时集训(三十四)平面向量的数量积与平面向量应用举例课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练301A组基础巩固练课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练31352468791011一、选择题1.(2018·全国卷Ⅱ)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=()A.4B.3C.2D.0B[a·(2a-b)=2a2-a·b=2-(-1)=3,故选B.]课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练321345687910112.已知平面向量a=(-2,3),b=(1,2),向量λa+b与b垂直,则实数λ的值为()A.413B.-413C.54D.-54课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练32134568791011D[ a=(-2,3),b=(1,2),∴λa+b=(-2λ+1,3λ+2). λa+b与b垂直,∴(λa+b)·b=0,∴(-2λ+1,3λ+2)·(1,2)=0,即-2λ+1+6λ+4=0,解得λ=-54.]课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练331245687910113.(多选)已知向量a=(1,-1),b=(2,x),设a与b的夹角为α,则()A.若a∥b,则x=-2B.若x=1,则|b-a|=5C.若x=-1,则a与b的夹角为60°D.若a+2b与a垂直,则x=3课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练33124568791011ABD[由a∥b可得x=-2,故A正确;若x=1,则b=(2,1),|b-a|=|(2,1)-(1,-1)|=12+22=5,故B正确;当x=-1时,cos〈a,b〉=a·b|a||b|=2+12×5=31010≠12,故C错误;a+2b=(5,-1+2x),由5+(-1)(-1+2x)=0,解得x=3,故D正确.]课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练341235687910114.(2020·武汉模拟)已知向量|a|=2,向量a与b夹角为3π4,且a·b=-1,则|a-b|=()A.5B.2C.2D.4课后限时集训(三十四)平面向量的数量积与平面向量应用举例1A组基础巩固练B组综合运用练2C组思维拓展练34123568791011A[由平面向量数量积的定义可知,a·b=|a|·|b|·cos3π4=2·|b|·-22=-1,∴|b|=1,∴|a-b|=|a-b|2=|a|2-2a·b+|b|2=2-2×-1+1=5.故选A.]课后限时集训(三十四)...