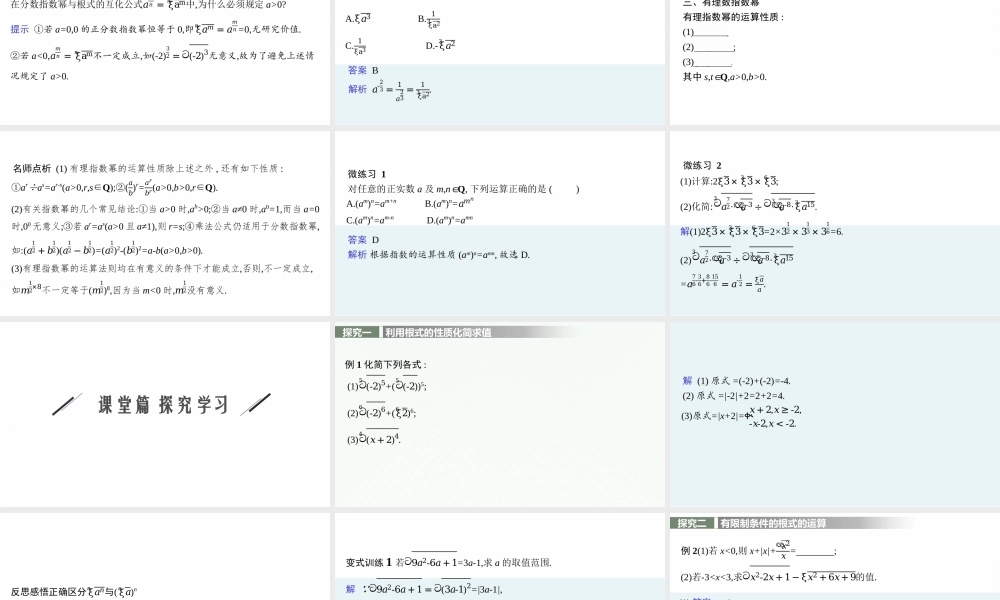
高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI4.1.1根式4.1.2指数幂的拓展第4章2021内容索引0102课前篇自主预习课堂篇探究学习课标阐释思维脉络1.理解根式和分数指数幂的概念.(数学抽象)2.掌握分数指数幂的运算性质,正确地进行各种指数运算.(数学运算)3.熟练进行根式和分数指数幂的互化.(数学运算)课前篇自主预习情境导入公元前五世纪,古希腊有一个数学学派名叫毕达哥拉斯学派,其学派中的一个成员希帕索斯考虑了一个问题:边长为1的正方形其对角线长度是多少呢?他发现这一长度既不能用整数,也不能用分数来表示,希帕索斯的发现导致了数学史上第一个无理数的诞生.若x2=3,这样的x有几个?它们叫作3的什么?怎么表示?ξ2希帕索斯知识点拨一、根式1.n次方根的定义一般地,如果xn=a(n>1,n∈N*),那么称x为a的n次方根.0的n次方根等于0.2.根式的定义式子叫作根式,其中n叫作根指数,a叫作被开方数.ξa𝑛3.根式的性质对于n∈N*,n>1,当n为奇数时,ξ𝑎𝑛𝑛=a;当n为偶数时,ξ𝑎𝑛𝑛=|a|=ቊ𝑎,𝑎≥0,-𝑎,𝑎<0.微思考(1)(ξa𝑛)n的含义是什么?(2)(ξ𝑎𝑛)n中实数a的取值范围是任意实数吗?提示(1)()n是实数a的n次方根的n次幂.(2)不一定,当n为大于1的奇数时,a∈R;当n为大于1的偶数时,a≥0.ξa𝑛二、分数指数幂名师点析关于分数指数幂要注意以下几点:(1)分数指数幂𝑎𝑚𝑛不可以理解为𝑚𝑛个a相乘,事实上,它是根式的一种新写法.(2)0的指数幂:0的正分数指数幂为0,0的负分数指数幂没有意义.微思考在分数指数幂与根式的互化公式𝑎𝑚𝑛=ξam𝑛中,为什么必须规定a>0?提示①若a=0,0的正分数指数幂恒等于0,即ξ𝑎𝑚𝑛=𝑎𝑚𝑛=0,无研究价值.②若a<0,𝑎𝑚𝑛=ξam𝑛不一定成立,如(-2)32=ට(-2)3无意义,故为了避免上述情况规定了a>0.微练习已知a>0,则𝑎-23等于()A.ξ𝑎3B.1ξa23C.1ξa3D.-ξ𝑎23答案B解析𝑎-23=1𝑎23=1ξa23.三、有理数指数幂有理指数幂的运算性质:(1)asat=as+t;(2)=ast;(3)(ab)t=atbt.其中s,t∈Q,a>0,b>0.(𝑎𝑠)𝑡名师点析(1)有理指数幂的运算性质除上述之外,还有如下性质:①ar÷as=ar-s(a>0,r,s∈Q);②(𝑎𝑏)r=𝑎𝑟𝑏𝑟(a>0,b>0,r∈Q).(2)有关指数幂的几个常见结论:①当a>0时,ab>0;②当a≠0时,a0=1,而当a=0时,00无意义;③若ar=as(a>0且a≠1),则r=s;④乘法公式仍适用于分数指数幂,如:(𝑎12+𝑏12)(𝑎12−𝑏12)=(𝑎12)2-(𝑏12)2=a-b(a>0,b>0).(3)有理指数幂的运算法则均在有意义的条件下才能成立,否则,不一定成立,如𝑚12×8不一定等于(𝑚12)8,因为当m<0时,𝑚12没...