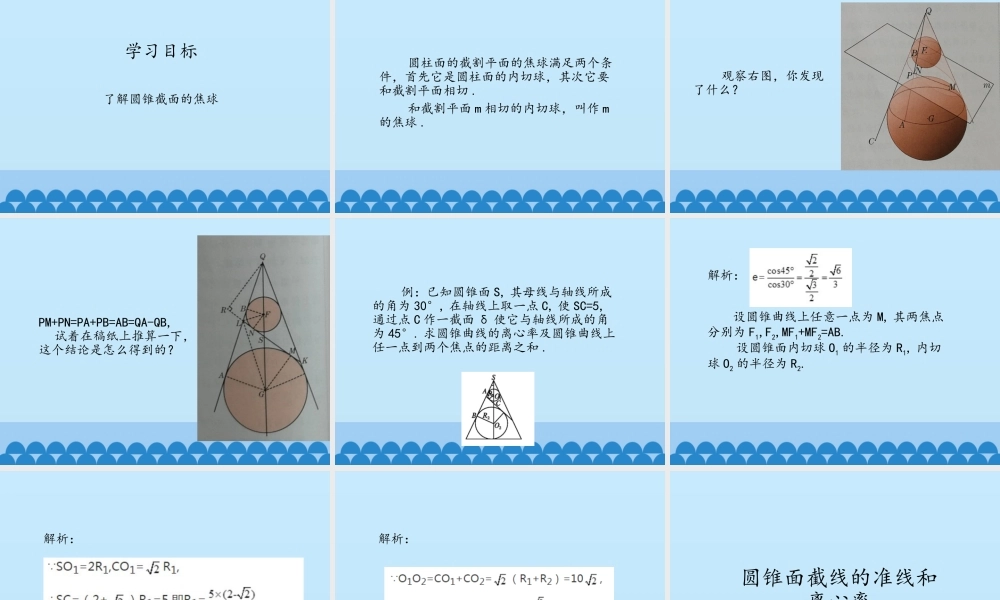
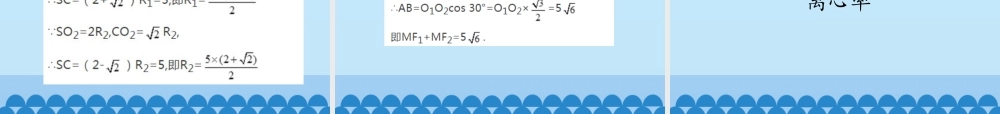圆锥面和圆锥曲线设空间有一条定曲线Σ和不在Σ上的一定点A,动点P在Σ上运动时,直线AP上的点的轨迹,叫做以A为顶点,以Σ为准线的锥面.每条直线AP都叫做此锥面的母线.一、锥面和柱面的定义对比一下:柱面是由一些相互平行的直线上的点组成的曲面,而锥面是由一些经过同一点的直线上的点组成的曲面.圆锥面若锥面的准线为一圆,锥面的顶点在过圆心且垂直于圆所在的平面的直线上,则此锥面叫作圆锥面.过圆锥面的顶点和它的准线圆的圆心的直线,叫作此圆锥面的轴线.命题3.1圆锥面的轴线和每条母线所成的锐角相等;轴线上任一点到每条母线的距离相等.二、圆锥面的性质命题3.2圆锥顶点到正截面之间所截母线上的线段相等;正截面截圆锥的截线是圆,其半径等于dtanα,其中d是圆锥面顶点到正截面的距离,α是圆锥面的半顶角.二、圆锥面的性质命题3.3圆锥面的斜截面的轴面,垂直于它和正截面的交线.二、圆锥面的性质命题3.4(圆锥面截线定理)设圆锥面的半顶角为α,平面π不经过圆锥面的顶点,且和圆锥面的轴线交角为β,则:①β>α,平面π与圆锥的截线为椭圆;②β=α,平面π与圆锥的截线为抛物线;③β<α,平面π与圆锥的截线为双曲线.二、圆锥面的性质三、圆锥的斜截面和它的轴面三、圆锥的斜截面和它的轴面圆锥截面的焦球了解圆锥截面的焦球学习目标圆柱面的截割平面的焦球满足两个条件,首先它是圆柱面的内切球,其次它要和截割平面相切.和截割平面m相切的内切球,叫作m的焦球.观察右图,你发现了什么?PM+PN=PA+PB=AB=QA-QB,试着在稿纸上推算一下,这个结论是怎么得到的?例:已知圆锥面S,其母线与轴线所成的角为30°,在轴线上取一点C,使SC=5,通过点C作一截面δ使它与轴线所成的角为45°.求圆锥曲线的离心率及圆锥曲线上任一点到两个焦点的距离之和.解析:设圆锥曲线上任意一点为M,其两焦点分别为F1,F2,MF1+MF2=AB.设圆锥面内切球O1的半径为R1,内切球O2的半径为R2.解析:解析:圆锥面截线的准线和离心率学习目标了解圆锥面截线的准线定理上一节我们把研究圆柱面截线的双球法推广到了圆锥面.在研究圆柱面的截线性质时,我们还从一个焦球出发,引出了截线椭圆的准线和离心率,这样的研究方法能不能推广到圆锥面呢?思考:讨论这个问题的前提,是下列命题成立:命题3.5圆锥面的内切球和圆锥面的公共点组成一个圆,这个圆所在的平面垂直于圆锥面的轴线.命题3.6设圆锥面的斜截面m的焦球中心和圆锥面顶点在平面m的同侧;焦球切m于点F;m与轴面q所含...