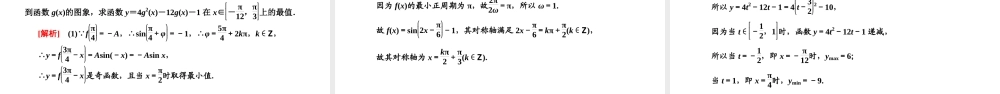习题课 三角函数.pptxVIP免费

综合考法(一)三角函数式的化简与求值【题型技法】[例1](1)已知tanα＋π4＝12，且－π2＜α＜0，则2sin2α＋sin2αcosα－π4等于()A．－255B．－3510C．－31010D.255(2)在△ABC中，若3cos2A－B2＋5sin2A＋B2＝4，则tanAtanB＝________.[解析](1)因为tanα＋π4＝tanα＋11－tanα＝12，所以tanα＝－13，因为－π2＜α＜0，所以sinα＝－1010，所以2sin2α＋sin2αcosα－π4＝2sinαsinα＋cosα22cosα＋sinα＝22sinα＝22×－1010＝－255.(2)因为3cos2A－B2＋5sin2A＋B2＝4，所以32cos(A－B)－52cos(A＋B)＝0，所以32cosAcosB＋32sinAsinB－52cosAcosB＋52sinAsinB＝0，即cosAcosB＝4sinAsinB，所以tanAtanB＝14.[答案](1)A(2)14[方法技巧]三角函数求值主要有三种类型(1)“给角求值”，一般给出的角都是非特殊角，从表面看较难，但仔细观察就会发现这类问题中的角与特殊角都有一定的关系，如和或差为特殊角，当然还有可能需要运用诱导公式．(2)“给值求值”，即给出某些角的三角函数式的值，求另外一些三角函数的值，这类求值问题关键在于结合条件和结论中的角，合理拆、配角．当然在这个过程中要注意角的范围．(3)“给值求角”，本质上还是“给值求值”，只不过往往求出的是特殊角的值，在求出角之前还需结合函数的单调性确定角，必要时还要讨论角的范围．【集训冲关】1．已知角θ的终边在直线y＝－2x上，则cos2θ的值为()A.35B.34C．－34D．－35解析：根据角θ的终边在直线y＝－2x上知，tanθ＝－2，所以cos2θ＝cos2θ－sin2θ＝cos2θ－sin2θsin2θ＋cos2θ＝1－tan2θtan2θ＋1＝1－－22－22＋1＝－35.答案：D2.17世纪德国著名的天文学家开普勒曾经这样说过：“几何学里有两件宝，一个是勾股定理，另一个是黄金分割．如果把勾股定理比作黄金矿的话，那么可以把黄金分割比作钻石矿．”黄金三角形有两种，其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形，它是一个顶角为36°的等腰三角形(另一种是顶角为108°的等腰三角形)．例如，五角星由五个黄金三角形与一个正五边形组成，如图所示，在其中一个黄金△ABC中，BCAC＝5－12.根据这些信息，可得sin234°的值为()A.1－254B．－3＋58C．－5＋14D．－4＋58解析：由图可知，∠ACB＝72°，且cos72°＝12BCAC＝5－14，∴cos144°＝2cos272°－1＝－5＋14.则sin234°＝sin(144°＋90°)＝cos144°＝...