0528高二数学（选修-人教B版）-导数复习（2）-2ppt.pptxVIP免费

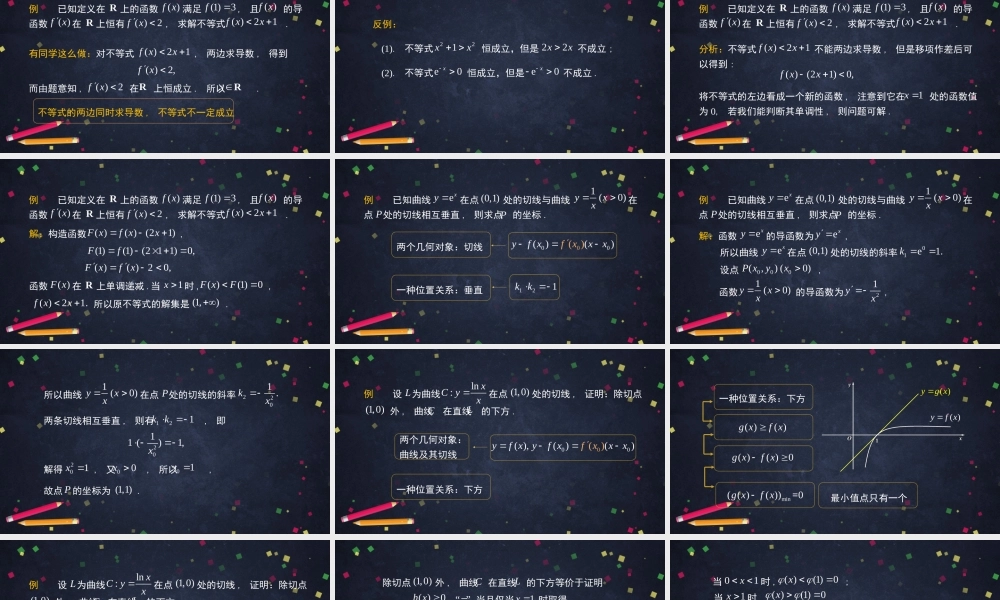
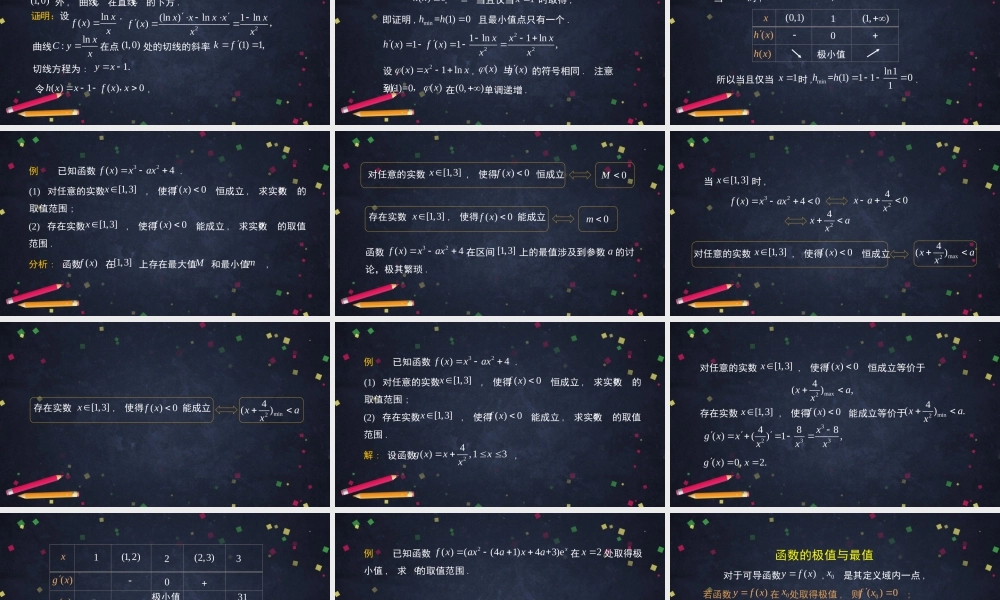
导数复习(2)高二年级数学主讲人：何效员北京一零一中学例已知定义在上的函数满足,且的导函数在上恒有,求解不等式.R()fx(1)3f()fx()fxR()2fx()21fxx有同学这么做：对不等式,两边求导数,得到()21fxx()2,fx而由题意知,在上恒成立.所以.()2fxRRx不等式的两边同时求导数,不等式不一定成立(1).不等式恒成立，但是不成立;(2).不等式恒成立，但是不成立.反例：221xx22xxe0xe0x例已知定义在上的函数满足,且的导函数在上恒有,求解不等式.R()fx(1)3f()fx()fxR()2fx()21fxx分析：不等式不能两边求导数,但是移项作差后可以得到:()21fxx()(21)0,fxx将不等式的左边看成一个新的函数,注意到它在处的函数值为0,若我们能判断其单调性,则问题可解.1x例已知定义在上的函数满足,且的导函数在上恒有,求解不等式.R()fx(1)3f()fx()fxR()2fx()21fxx解：构造函数,()()(21)Fxfxx(1)(1)(211)0,Ff()()2Fxfx0,函数在上单调递减.当时,,所以原不等式的解集是.()FxR1x()(1)0FxF()21.fxx(1,)例已知曲线在点处的切线与曲线在点处的切线相互垂直,则求点的坐标.exy(0,1)1(0)yxxPP两个几何对象：切线一种位置关系：垂直000)(()()yfxxxxf121kk例已知曲线在点处的切线与曲线在点处的切线相互垂直,则求点的坐标.exy(0,1)1(0)yxxPP解：函数的导函数为,exy所以曲线在点处的切线的斜率exyexy(0,1)01e1.k设点,000(,)(0)Pxyx函数的导函数为,1(0)yxx21yx所以曲线在点处的切线的斜率1(0)yxxP2201.kx两条切线相互垂直,则有,即121kk2011()1,x解得,又,所以,故点的坐标为.201x00x01xP(1,1)例设为曲线在点处的切线,证明：除切点外,曲线在直线的下方.Lln:xCyx(1,0)(1,0)LC两个几何对象：曲线及其切线一种位置关系：下方000(),()()()yfxfxyfxxx()()gxfx最小值点只有一个()()0gxfxmin(()())0=gxfx一种位置关系：下方()ygx()yfx切线方程为:例设为曲线在点处的切线,证明：除切点外,曲线在直线的下方.Lln:xCyx(1,0)(1,0)LC1.yx证明：设,ln()xfxx22(ln)ln1ln()xxxxxfxxx，曲线在点处的切线的斜率ln:xCyx(1,0)(1)1,kf令,()1()0hxxfxx，设,与的符号相同.注意到：除切点外,曲线在直线的下方等价于证明,当且仅当时取得,(1,0)CL即证明,...