1.4.2 第1课时.pptxVIP免费

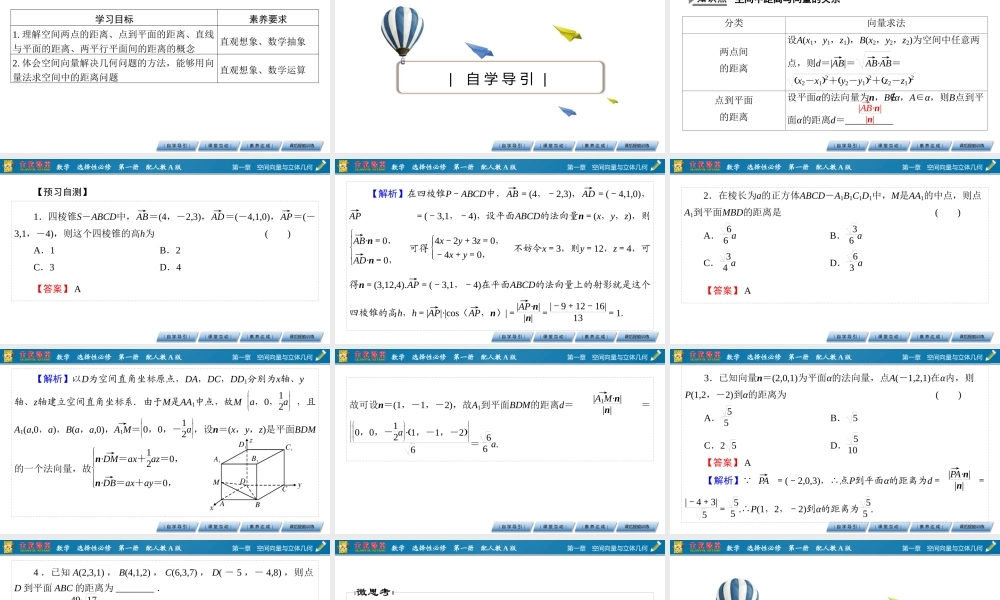
第一章空间向量与立体几何1.4空间向量的应用1.4.2用空间向量研究距离、夹角问题第1课时空间中的距离问题第一章空间向量与立体几何数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练学习目标素养要求1.理解空间两点的距离、点到平面的距离、直线与平面的距离、两平行平面间的距离的概念直观想象、数学抽象2.体会空间向量解决几何问题的方法，能够用向量法求空间中的距离问题直观想象、数学运算第一章空间向量与立体几何数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练|自学导引|第一章空间向量与立体几何数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练空间中距离与向量的关系分类向量求法两点间的距离设A(x1，y1，z1)，B(x2，y2，z2)为空间中任意两点，则d＝|AB→|＝AB→·AB→＝x2－x12＋y2－y12＋z2－z12点到平面的距离设平面α的法向量为n，B∉α，A∈α，则B点到平面α的距离d＝__________|AB→·n||n|第一章空间向量与立体几何数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练【答案】A【预习自测】1．四棱锥S－ABCD中，AB→＝(4，－2,3)，AD→＝(－4,1,0)，AP→＝(－3,1，－4)，则这个四棱锥的高h为()A．1B．2C．3D．4第一章空间向量与立体几何数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练【解析】在四棱锥P－ABCD中，AB→＝(4，－2,3)，AD→＝(－4,1,0)，AP→＝(－3,1，－4)，设平面ABCD的法向量n＝(x，y，z)，则AB→·n＝0，AD→·n＝0，可得4x－2y＋3z＝0，－4x＋y＝0，不妨令x＝3，则y＝12，z＝4，可得n＝(3,12,4).AP→＝(－3,1，－4)在平面ABCD的法向量上的射影就是这个四棱锥的高h，h＝|AP→|·|cos〈AP→，n〉|＝|AP→·n||n|＝|－9＋12－16|13＝1.第一章空间向量与立体几何数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练【答案】A2．在棱长为a的正方体ABCD－A1B1C1D1中，M是AA1的中点，则点A1到平面MBD的距离是()A．66aB．36aC．34aD．63a第一章空间向量与立体几何数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练【解析】以D为空间直角坐标原点，DA，DC，DD1分别为x轴、y轴、z轴建立空间直角坐标系．由于M是AA1中点，故Ma，0，12a，且A1(a,0，a)，B(a，a,0)，A1M→＝0...