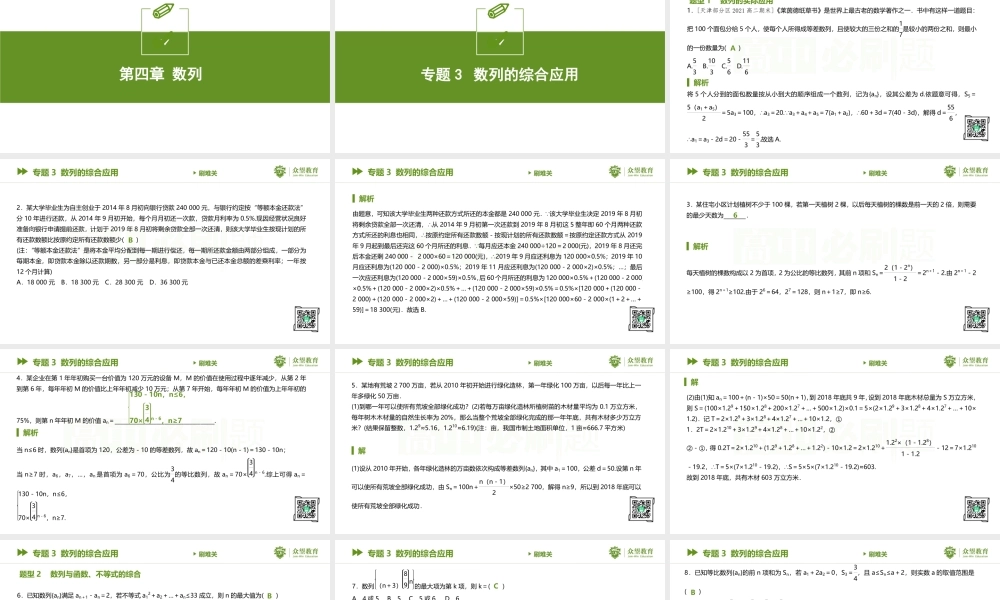
数学选修2RJA04第四章数列04专题3数列的综合应用题型1数列的实际应用解析专题3数列的综合应用刷难关A1.[天津部分区2021高二期末]《莱茵德纸草书》是世界上最古老的数学著作之一.书中有这样一道题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的17是较小的两份之和,则最小的一份数量为()A.53B.103C.56D.116将5个人分到的面包数量按从小到大的顺序组成一个数列,记为{an},设其公差为d.依题意可得,S5=5(a1+a5)2=5a3=100,∴a3=20. a3+a4+a5=7(a1+a2),∴60+3d=7(40-3d),解得d=556,∴a1=a3-2d=20-553=53.故选A.专题3数列的综合应用刷难关B2.某大学毕业生为自主创业于2014年8月初向银行贷款240000元,与银行约定按“等额本金还款法”分10年进行还款,从2014年9月初开始,每个月月初还一次款,贷款月利率为0.5%.现因经营状况良好准备向银行申请提前还款,计划于2019年8月初将剩余贷款全部一次还清,则该大学毕业生按现计划的所有还款数额比按原约定所有还款数额少()(注:“等额本金还款法”是将本金平均分配到每一期进行偿还,每一期所还款金额由两部分组成,一部分为每期本金,即贷款本金除以还款期数,另一部分是利息,即贷款本金与已还本金总额的差乘利率;一年按12个月计算)A.18000元B.18300元C.28300元D.36300元解析专题3数列的综合应用刷难关由题意,可知该大学毕业生两种还款方式所还的本金都是240000元. 该大学毕业生决定2019年8月初将剩余贷款全部一次还清,∴从2014年9月初第一次还款到2019年8月初这5整年即60个月两种还款方式所还的利息也相同,∴按原约定所有还款数额-按现计划的所有还款数额=按原约定还款方式从2019年9月起到最后还完这60个月所还的利息. 每月应还本金240000÷120=2000(元),2019年8月还完后本金还剩240000-2000×60=120000(元),∴2019年9月应还利息为120000×0.5%;2019年10月应还利息为(120000-2000)×0.5%;2019年11月应还利息为(120000-2000×2)×0.5%;…;最后一次应还利息为(120000-2000×59)×0.5%,后60个月所还的利息为120000×0.5%+(120000-2000)×0.5%+(120000-2000×2)×0.5%+…+(120000-2000×59)×0.5%=0.5%×[120000+(120000-2000)+(120000-2000×2)+…+(120000-2000×59)]=0.5%×[120000×60-2000×(1+2+…+59)]=18300(元).故选B.解析专题3数列的综合应用刷难关63.某住宅小区计划植树不少于100棵,若第一...