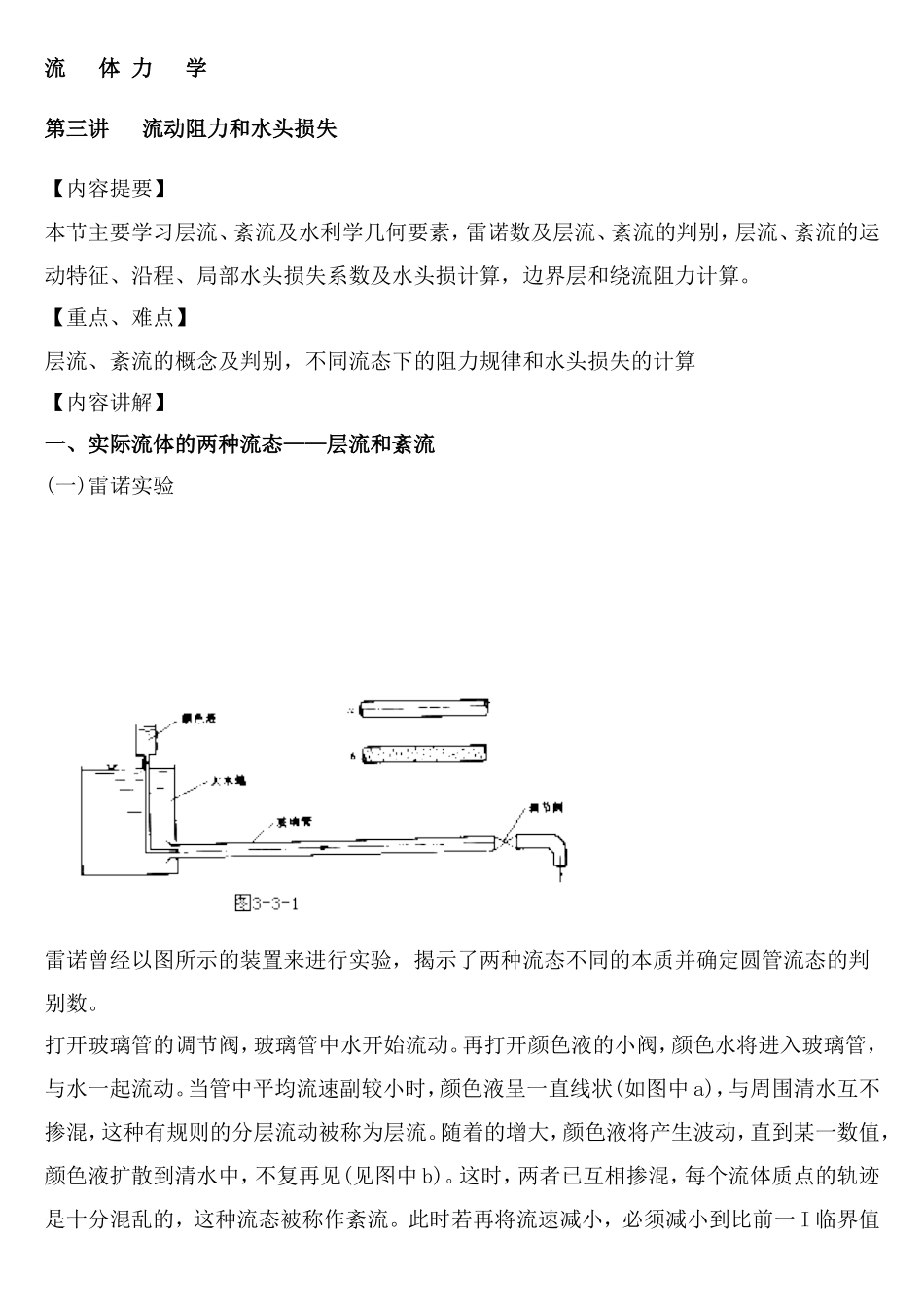
流体力学第三讲流动阻力和水头损失【内容提要】本节主要学习层流、紊流及水利学几何要素,雷诺数及层流、紊流的判别,层流、紊流的运动特征、沿程、局部水头损失系数及水头损计算,边界层和绕流阻力计算。【重点、难点】层流、紊流的概念及判别,不同流态下的阻力规律和水头损失的计算【内容讲解】一、实际流体的两种流态——层流和紊流(一)雷诺实验雷诺曾经以图所示的装置来进行实验,揭示了两种流态不同的本质并确定圆管流态的判别数。打开玻璃管的调节阀,玻璃管中水开始流动。再打开颜色液的小阀,颜色水将进入玻璃管,与水一起流动。当管中平均流速副较小时,颜色液呈一直线状(如图中a),与周围清水互不掺混,这种有规则的分层流动被称为层流。随着的增大,颜色液将产生波动,直到某一数值,颜色液扩散到清水中,不复再见(见图中b)。这时,两者已互相掺混,每个流体质点的轨迹是十分混乱的,这种流态被称作紊流。此时若再将流速减小,必须减小到比前一I临界值更小的数值,流态才会转变为层流。层流和紊流由于两者内部结构不同,能量损失的规律也不同。由实验得到:直管上下游断面间的水头损失,层流时与断面平均流速的一次方成正比,紊流时则与流速的1.75~2.0次方成正比,(二)层流和紊流的判别数——雷诺数由于层流和紊流水头损失的规律不同,在计算水头损失前,必须判别流态。流态的确定除了与流速的大小有关外,还与管径和流体的粘性有关。因此采用综合性的雷诺数Re作为判别流态的无量纲数。二、圆管中的层流运动(一)均匀流动方程式取一段等直径圆管中的恒定均匀流来讨论,见图3-3-2。三、紊流运动的特征紊流中,流体质点在运动中不断互相混杂,使各点的流速、压强等运动要素都随时间作无规则的变化,这种变化称为脉动现象。这种脉动是围绕某一平均值而变化的。这样,可以将紊流看作两个流动的叠加。即时间平均流动和脉动的叠加。引入时间平均流动的概念后,尽管紊流实质上是极无规则的非恒定流,但只要它的时均值是一常数就可以将它看成恒定流。或者它的时均值随时间遵循某一规律变化,就可看作是随时间遵循某一规律变化的非恒定流(如水箱中水无补给时,经水箱孔口的出流),而且前面提到的概念如流线、断面平均流速等等对于时间平均流动,仍可照常应用。但对于紊流的切应力、紊流扩散等问题的研究却必须考虑紊流的脉动。紊流中的切应力除了由于粘性所产生的切应力外,由于质点互相掺混、动量的交换,还存在着紊流的附加切应力,又称为雷诺...