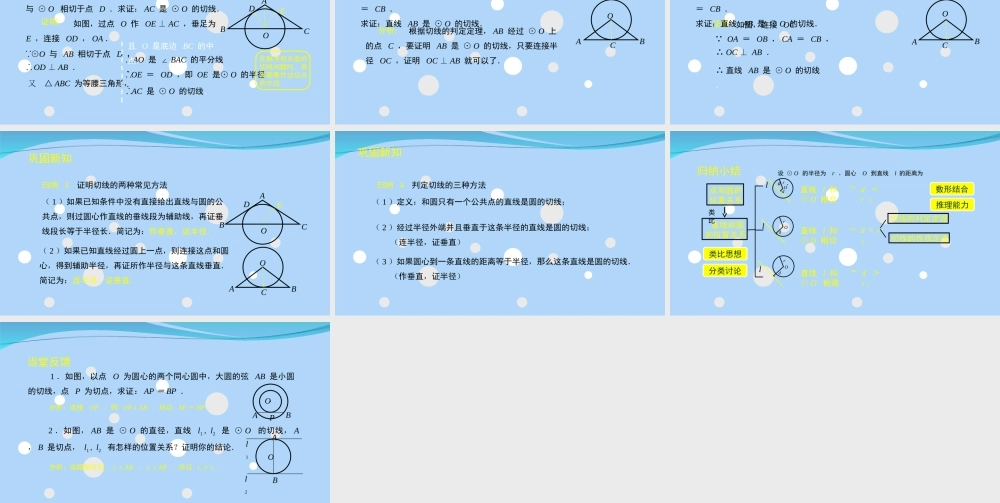
人教版九年级上册数学24.2.2直线和圆的位置关系(2)探究新知生活实例思考1如图,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离与圆的半径有什么数量关系?直线l和⊙O有什么位置关系?由此你发现了什么?探究新知OAl归纳1(1)直线l经过半径OA的外端A;(2)直线l垂直于半径OA,则直线与⊙O相切.圆心O到直线l的距离等于圆的半径;相切.切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.探究新知符号语言⸪OA是⊙O的半径,直线l⊥OA于点A,⸫直线l是⊙O的切线.OAlOAlOAl探究新知问题已知一个圆和圆上一点,如何过这个点作出圆的切线?分析:连接圆心和圆上这一点,得到圆的半径;过圆上这点作这条半径的垂线即为过圆上这一点作出的此圆的切线.思考2如图,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?探究新知OAl切线的性质定理圆的切线垂直于过切点的半径.一定垂直符号语言⸫直线l⊥OA.⸪直线l是⊙O的切线,点A为切点,归纳2切线的性质(1)切线和圆有且只有一个公共点;Al归纳2切线的性质(1)切线和圆有且只有一个公共点;(2)圆心到切线的距离等于半径;(3)圆的切线垂直于过切点的半径;OAl归纳2切线的性质探究新知(1)切线和圆有且只有一个公共点;(2)圆心到切线的距离等于半径;(3)圆的切线垂直于过切点的半径;(4)经过圆心垂直于切线的直线必过切点;(5)经过切点垂直于切线的直线必过圆心.AlO例1如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.深化新知OABCD分析:E切线半径垂线段例1如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.三、深化新知如图,过点O作OE⊥AC,垂足为E,连接OD,OA.证明:⸪⊙O与AB相切于点D,⸫OD⊥AB.又△ABC为等腰三角形,⸫AO是∠BAC的平分线.⸫OE=OD,即OE是⊙O的半径.⸫AC是⊙O的切线.辅助线:(无公共点)作垂直,证半径.ABCDE且O是底边BC的中点,在解决有关圆的切线问题时,常常需要作过切点的半径.O巩固新知OABC根据切线的判定定理,AB经过⊙O上的点C,要证明AB是⊙O的切线,只要连接半径OC,证明OC⊥AB就可以了.分析:练习1如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.巩固新知OABC证明:如图,连接OC. OA=OB,CA=CB,∴OC⊥AB.∴直线AB是⊙O的切线.辅助线:(有公共点)连半径,证垂直.练习1如图...