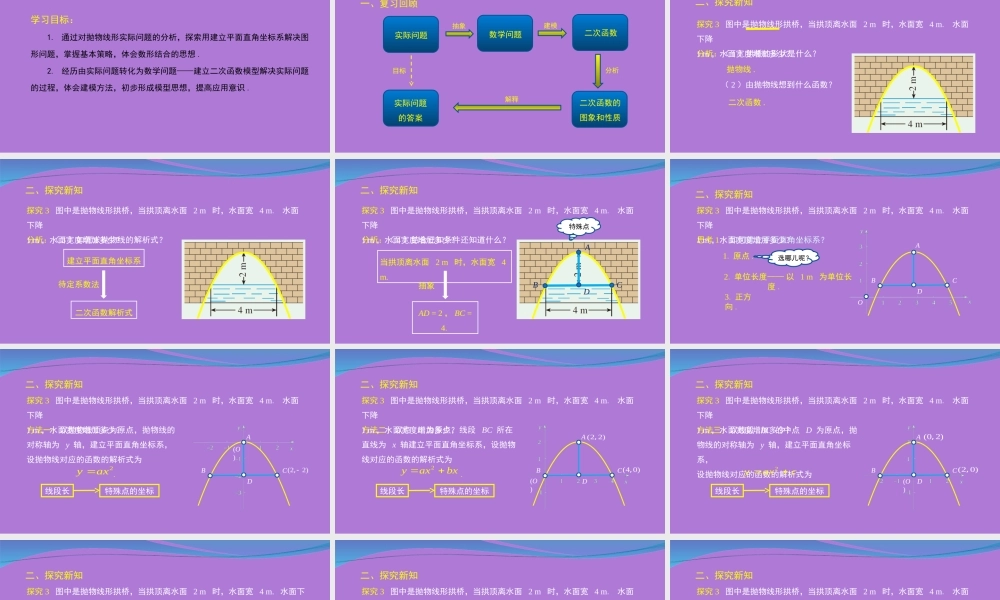
人教版九年级上册数学22.3实际问题与二次函数(3)学习目标:1.通过对抛物线形实际问题的分析,探索用建立平面直角坐标系解决图形问题,掌握基本策略,体会数形结合的思想.2.经历由实际问题转化为数学问题——建立二次函数模型解决实际问题的过程,体会建模方法,初步形成模型思想,提高应用意识.二次函数的图象和性质一、复习回顾实际问题二次函数实际问题的答案目标数学问题抽象建模分析解释分析:(1)拱桥的形状是什么?抛物线.探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?二、探究新知(2)由抛物线想到什么函数?二次函数.分析:(3)如何求抛物线的解析式?建立平面直角坐标系二、探究新知二次函数解析式待定系数法探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?当拱顶离水面2m时,水面宽4m.特殊点AC分析:(4)结合已知条件还知道什么?二、探究新知BDAD=2,BC=4.抽象探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?思考1如何建立平面直角坐标系?1.原点.2.单位长度——以1m为单位长度.选哪儿呢?O3.正方向.二、探究新知ACBD探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?方法一:以抛物线顶点为原点,抛物线的对称轴为y轴,建立平面直角坐标系,设抛物线对应的函数的解析式为.2yax二、探究新知线段长特殊点的坐标A(O)(22),CBD探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?方法二:以点B为原点,线段BC所在直线为x轴建立平面直角坐标系,设抛物线对应的函数的解析式为.2yaxbx二、探究新知线段长特殊点的坐标BCA(O)(22),(40),D探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?方法三:以线段BC的中点D为原点,抛物线的对称轴为y轴,建立平面直角坐标系,设抛物线对应的函数的解析式为.2yaxc二、探究新知线段长特殊点的坐标BCAD(O)(02),(20),探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?2yaxbx2yaxc2yax图2图3图1二、探究新知探究3图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?分析:(5)求宽度增加多少需要什么数据?二、探究新知点E和点F的横坐标.(6)怎样求出表示水面宽度线段的端点横坐...