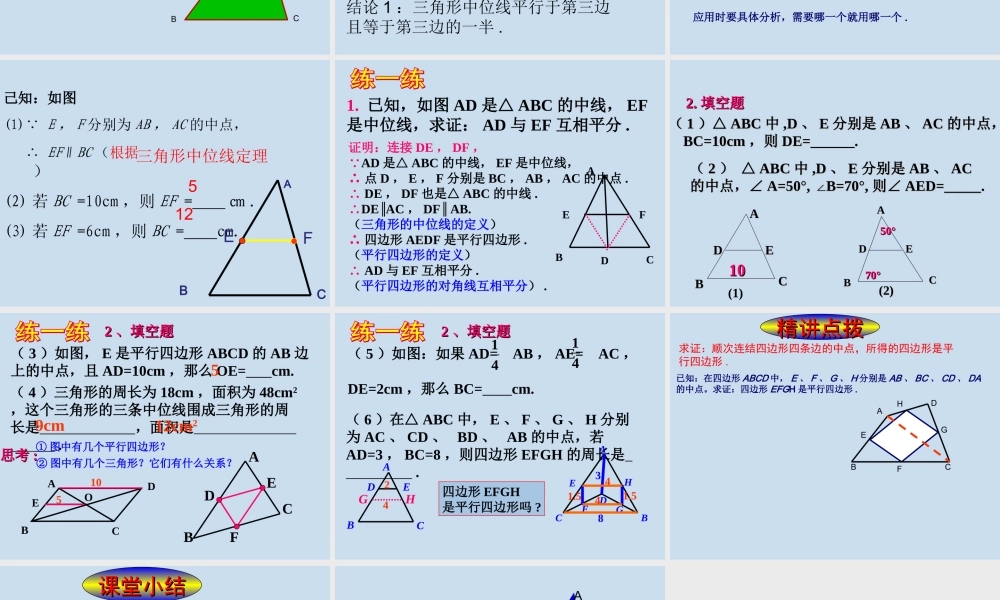
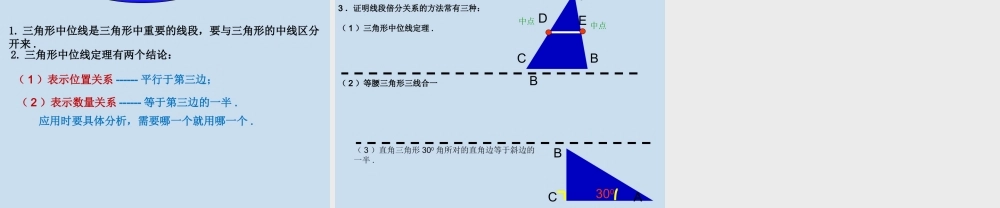
八年级数学上册第五章平行四边形1.掌握三角形中位线的概念;2.了解三角形中位线的性质定理及其证明方法;3.学会运用三角形中位线的性质定理解决问题.教学目标教学目标三角形的中线三角形的中线ABC在三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线.顶点顶点D中点DE称三角形的做什么呢?E中点它就是我们这节课要学习的三角形的中位线。知识回顾知识回顾1.你能给“三角形中位线”下一个定义吗?ABC中点D中点E2.一个三角形有几条中位线?3.三角形的中位线与中线有什么区别?答:三条。答:中位线是连结三角形两边中点的线段;中线是连结一个顶点和它的对边中点的线段.F定义:连结三角形两边中点的线段叫做三角形的中位线.ABC4.三角形中位线有什么特殊的性质?中点D中点E猜想1:DE//BC猜想2:DE=BC21合作探究合作探究结论1:三角形中位线平行于第三边且等于第三边的一半.ABCDE已知:如图,DE是△ABC的中位线.求证:DEBCDE=BC.∥ABCDE三角形中位线定理:三角形中位线平行于第三边,并且等于它的一半.三角形中位线定理有两个结论:(1)表示位置关系------平行于第三边;(2)表示数量关系------等于第三边的一半.应用时要具体分析,需要哪一个就用哪一个.己知:如图(1) E,F分别为AB,AC的中点,∴EF∥BC(根据)(2)若BC=10cm,则EF=㎝.(3)若EF=6cm,则BC=cm.ABCEF三角形中位线定理512证明:连接DE,DF, AD是△ABC的中线,EF是中位线,∴点D,E,F分别是BC,AB,AC的中点.∴DE,DF也是△ABC的中线.∴DE∥AC,DF∥AB.(三角形的中位线的定义)∴四边形AEDF是平行四边形.(平行四边形的定义)∴AD与EF互相平分.(平行四边形的对角线互相平分).1.已知,如图AD是△ABC的中线,EF是中位线,求证:AD与EF互相平分.ABCDEF((11)△)△ABCABC中中,D,D、、EE分别是分别是ABAB、、ACAC的中点,的中点,BC=10cmBC=10cm,则,则DE=______.DE=______.AAEEDDCCBB(1)BBDDAAEECC(2)(2)((22)△)△ABCABC中中,D,D、、EE分别是分别是ABAB、、ACAC的中点,∠的中点,∠A=50°,B=70°,∠A=50°,B=70°,∠则∠则∠AED=_____.AED=_____.2.2.填空题填空题101050°50°70°70°(4)三角形的周长为18cm,面积为48cm2,这个三角形的三条中位线围成三角形的周长是,面积是.(3)如图,E是平行四边形ABCD的AB边上的中点,且AD=10cm,那么OE=cm.ABDCEO522、填空题、填空题FEABCD9cm10512cm2①图中有几个平行四边形?②图中有几个三角形?它们有什么关系?思考...