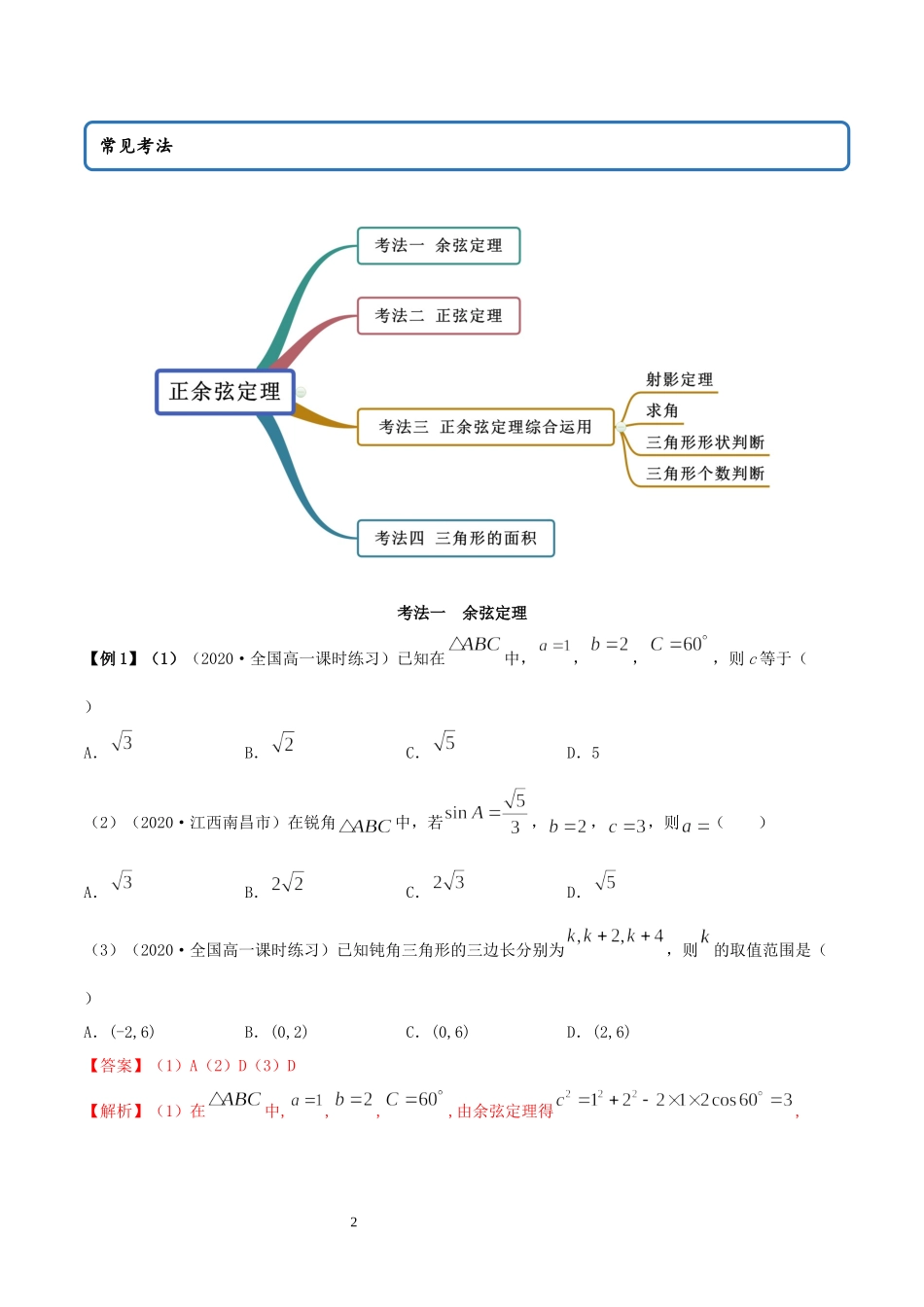
16.4.2正余弦定理(精讲)思维导图2考法一余弦定理【例1】(1)(2020·全国高一课时练习)已知在中,,,,则c等于()A.B.C.D.5(2)(2020·江西南昌市)在锐角中,若,,,则()A.B.C.D.(3)(2020·全国高一课时练习)已知钝角三角形的三边长分别为,则的取值范围是()A.(-2,6)B.(0,2)C.(0,6)D.(2,6)【答案】(1)A(2)D(3)D【解析】(1)在中,,,,由余弦定理得,常见考法3所以.故选:A(2)因为为锐角三角形,由同角三角函数关系式可得又因为,由余弦定理可得代入可得所以故选:D(3)由题:钝角三角形的三边长分别为解得:.故选:D【跟踪训练】1.(2020·全国高一)在△ABC中,内角A,B,C的对边分别为a,b,c,右a=1,c=2,∠B=600,则b=()A.1B.C.D.2【答案】C【解析】因为,,,则由余弦定理可得.故选:.2.(2020·全国高一课时练习)在中,内角,,所对的边分别为,,,且,则此三角形中的最大角的大小为()A.B.C.D.【答案】B【解析】中设,4由余弦定理可得.因为为三角形的内角,所以此三角形中的最大角,故选:B.3.(2020·北京人大附中高一期末)在中,,,,则等于()A.B.3C.D.21【答案】A【解析】因为,,,所以,即,故选:A.考法二正弦定理【例2】(1)(2020·辽宁锦州市·高一期末)在中,内角,,的对边分别为,,,,,,则角为()A.60°B.60°或120°C.45°D.45°或135°(2)(2020·湖北黄冈市·高一期末)在△ABC中,内角A,B,C的对边分别为,b,c,已知,,,则()A.B.C.D.(3)(2020·全国高一课时练习)已知△ABC的内角A,B,C的对边分别为a,b,c,若A=60°,a5,则等于()A.B.C.D.2【答案】(1)B(2)B(3)D【解析】(1)由正弦定理得得得,,,得或,故选:B.(2)因为,所以为钝角,,为锐角.由得,所以.故选:B.(3)A=60°,a,由正弦定理可得,2,∴b=2sinB,c=2sinC,则2.故选:D.【跟踪训练】1.(2020·和县第二中学)在中,,则()A.B.或C.D.【答案】B【解析】由正弦定理可得,,6,或.故选:B.2.(2020·吉林长春市实验中学)在中,若,,,则等于()A.B.或C.D.或【答案】D【解析】由题意,在中,由正弦定理可得,即,又由,且,所以或,故选:D.3.(2020·合肥市第十一中学高一期末)已知△ABC中,,则b等于()A.2B.1C.D.【答案】D【解析】由正弦定理,得.故选:D.4.(2020·眉山市彭山区第一中学高一期中)在中,角、、所对的边...