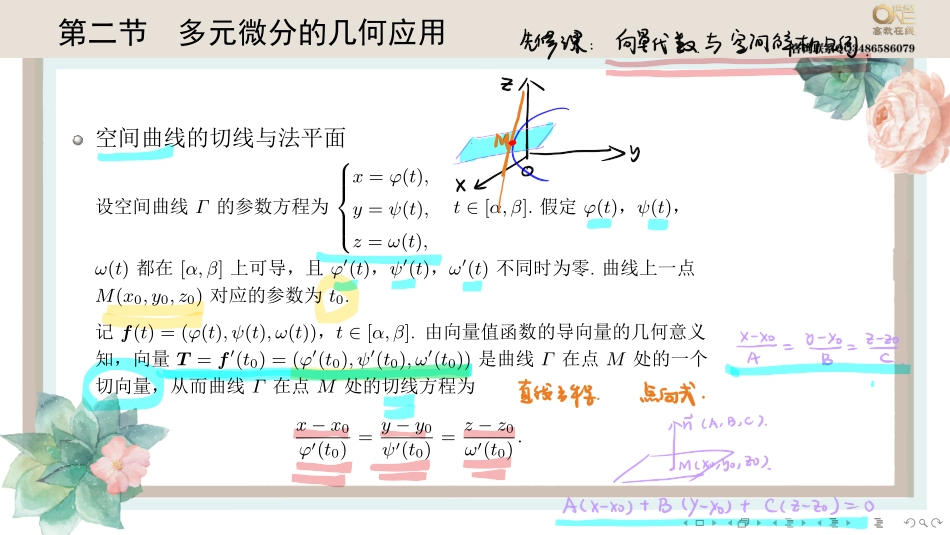
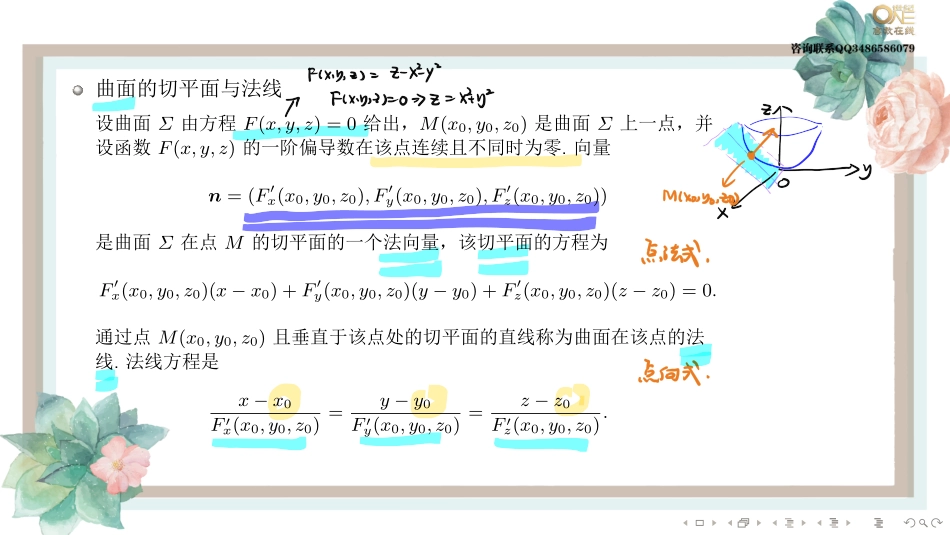
........第二节多元微分的几何应用空间曲线的切线与法平面设空间曲线Γ的参数方程为x=φ(t),y=ψ(t),z=ω(t),t∈[α,β].假定φ(t),ψ(t),ω(t)都在[α,β]上可导,且φ′(t),ψ′(t),ω′(t)不同时为零.曲线上一点M(x0,y0,z0)对应的参数为t0.记f(t)=(φ(t),ψ(t),ω(t)),t∈[α,β].由向量值函数的导向量的几何意义知,向量T=f′(t0)=(φ′(t0),ψ′(t0),ω′(t0))是曲线Γ在点M处的一个切向量,从而曲线Γ在点M处的切线方程为x−x0φ′(t0)=y−y0ψ′(t0)=z−z0ω′(t0)........通过点M且与切线垂直的平面称为曲线Γ在点M处的法平面,它是通过点M(x0,y0,z0)且以T=f′(t0)为法向量的平面,法平面方程为φ′(t0)(x−x0)+ψ′(t0)(y−y0)+ω′(t0)(z−z0)=0........曲面的切平面与法线设曲面Σ由方程F(x,y,z)=0给出,M(x0,y0,z0)是曲面Σ上一点,并设函数F(x,y,z)的一阶偏导数在该点连续且不同时为零.向量n=(F′x(x0,y0,z0),F′y(x0,y0,z0),F′z(x0,y0,z0))是曲面Σ在点M的切平面的一个法向量,该切平面的方程为F′x(x0,y0,z0)(x−x0)+F′y(x0,y0,z0)(y−y0)+F′z(x0,y0,z0)(z−z0)=0.通过点M(x0,y0,z0)且垂直于该点处的切平面的直线称为曲面在该点的法线.法线方程是x−x0F′x(x0,y0,z0)=y−y0F′y(x0,y0,z0)=z−z0F′z(x0,y0,z0).........例10..曲面z=x2+y2与平面2x+4y−z=0平行的切平面的方程是........方向导数设函数z=f(x,y)在点P0(x0,y0)的某个邻域U(P0)内有定义,射线l:x=x0+tcosα,y=y0+tcosβ(t≥0)以点P0为起点,P(x0+tcosα,y0+tcosβ)为射线l上另一点,且P∈U(P0).若函数增量f(x0+tcosα,y0+tcosβ)−f(x0,y0)与P到P0的距离|PP0|=t的比值f(x0+tcosα,y0+tcosβ)−f(x0,y0)t当P沿着l趋于P0(即t→0+)时的极限存在,则称此极限为函数f(x,y)在点P0处沿着方向l的方向导数,记作∂f∂l��(x0,y0),即∂f∂l����(x0,y0)=limt→0+f(x0+tcosα,y0+tcosβ)−f(x0,y0)t........梯度设函数f(x,y)在平面区域D内具有一阶连续偏导数,则对于每一点P0(x0,y0)∈D,都可定出一个向量f′x(x0,y0)i+f′y(x0,y0)j,该向量称为函数f(x,y)在点P0(x0,y0)的梯度,记作gradf(x0,y0)或∇f(x0,y0),即gradf(x0,y0)=∇f(x0,y0)=f′x(x0,y0)i+f′y(x0,y0)j,其中∇=∂∂xi+∂∂yj称为(二维的)向量微分算子或Nabla算子,∇f=∂f∂xi+∂f∂yj.三元函数的梯度可类似定义........方向导数存在的充分条件若函数f(x,y)在点P0(x0,y0)处可微分,el...