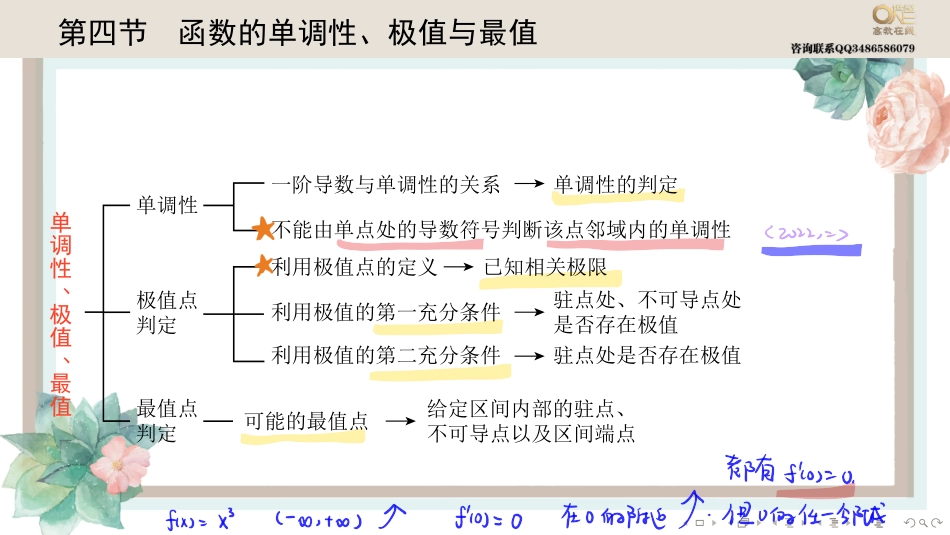
........第四节函数的单调性、极值与最值���������������������������������������������������������������������������������������������������������������������������������������������������.......函数的单调性与一阶导数的关系设函数f(x)在[a,b]上连续,在(a,b)内可导.若在(a,b)内f′(x)≥0,且等号只在有限个点处成立,则f(x)在[a,b]上单调增加.(单调减少的情况对应于f′(x)≤0的情况.).例15..设函数f(x)连续,且f′(0)>0,则存在δ>0,使得()(A)f(x)在(0,δ)内单调增加.(B)f(x)在(−δ,0)内单调减少.(C)对任意的x∈(0,δ),有f(x)>f(0).(D)对任意的x∈(−δ,0),有f(x)>f(0)...............【经典反例】单点处的导数符号不能决定该点邻域内的函数单调性b站@考研数学李艳芳.......极值点设函数f(x)在点x0的某邻域U(x0)内有定义.若对去心邻域◦U(x0)内的任一x,都有f(x)f(x0)),则称f(x0)是函数f(x)的一个极大值(或极小值).函数的极大值与极小值统称为函数的极值,使函数取得极值的点称为极值点.利用定义判断极值点极值点与最值点........例16..设函数f(x)在x=0的某邻域内连续,且limx→0f(x)xsinx=−2,则在x=0处f(x)()(A)不可导.(B)可导,且f′(0)̸=0.(C)取极大值.(D)取极小值........极值的判定条件必要条件设函数f(x)在x0处可导,且在x0处取得极值,则f′(x0)=0.第一充分条件设函数f(x)在x0处连续,且在x0的某去心邻域◦U(x0,δ)内可导.(1)若x∈(x0−δ,x0)时,f′(x)>0,而x∈(x0,x0+δ)时,f′(x)<0,则f(x)在x0处取得极大值.(2)若x∈(x0−δ,x0)时,f′(x)<0,而x∈(x0,x0+δ)时,f′(x)>0,则f(x)在x0处取得极小值.(3)若x∈◦U(x0,δ)时,f′(x)的符号保持不变,则f(x)在x0处没有极值........极值的判定条件第二充分条件设函数f(x)在x0处具有二阶导数且f′(x0)=0,f′′(x0)̸=0,则(1)当f′′(x0)<0时,函数f(x)在x0处取得极大值;(2)当f′′(x0)>0时,函数f(x)在x0处取得极小值..例17..当a为何值时,函数f(x)=asinx+13sin3x在x=π3处取得极值,它是极大值还是极小值,并求出此值................例18..作半径为r的球的外切正圆锥,问此圆锥的高h为何值时,其体积V最小,并求出该最小值........����见讲义第四节同步习题.