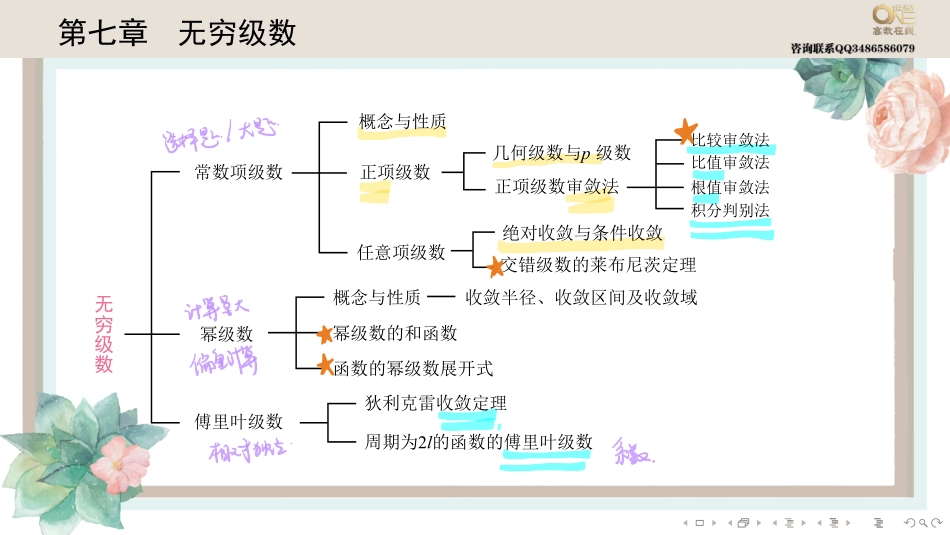
........第七章无穷级数�������������������������������p��������������������������������������������������������2l����������������������������������������������������........第一节常数项级数级数的基本概念(1)一般地,若给定一个数列a1,a2,···,an,···,则由该数列构成的表达式a1+a2+···+an+···称为(常数项)无穷级数,简称(常数项)级数,记为∞∑n=1an,其中an称为级数的一般项,前n项的和sn=a1+a2+···+an=n∑k=1ak称为级数∞∑n=1an的部分和.(2)若级数∞∑n=1an的部分和数列{sn}有极限s,即limn→∞sn=s,则称无穷级数∞∑n=1an收敛,此时s称为该收敛级数的和;若{sn}没有极限,则称无穷级数∞∑n=1an发散........收敛级数的重要性质(1)若∞∑n=1an为收敛级数,则∞∑n=1an=s⇒∞∑n=1can=cs.(2)若∞∑n=1an,∞∑n=1bn为收敛级数,则∞∑n=1an=s,∞∑n=1bn=t⇒∞∑n=1(an±bn)=s±t........(3)在级数中去掉、加上或改变有限项,不会改变级数的收敛性.(4)若级数∞∑n=1an收敛,对该级数的项任意添加括号,得到新级数(a1+···+an1)+(an1+1+···+an2)+···+(ank−1+1+···+ank)+···,则这个新级数仍收敛,且其和不变.(5)级数收敛的必要条件若级数∞∑n=1an收敛,则limn→∞an=0.........例1..已知级数∞∑n=1(−1)n−1an=2,∞∑n=1a2n−1=5,则级数∞∑n=1an等于()(A)3.(B)7.(C)8.(D)9........若limn→∞an=0,且∞∑n=1(a2n−1+a2n)收敛,则∞∑n=1an=∞∑n=1(a2n−1+a2n).视频:级数审敛的小细节b站@考研数学李艳芳.......正项级数审敛法(1)比较审敛法设∞∑n=1an和∞∑n=1bn都是正项级数,且an≤bn(n=1,2,···).若∞∑n=1bn收敛,则∞∑n=1an收敛;若∞∑n=1an发散,则∞∑n=1bn发散.(2)比较审敛法的极限形式设∞∑n=1an和∞∑n=1bn都是正项级数,•若limn→∞anbn=l(0≤l<+∞),且级数∞∑n=1bn收敛,则级数∞∑n=1an收敛;•若limn→∞anbn=l>0或limn→∞anbn=+∞,且级数∞∑n=1bn发散,则级数∞∑n=1an发散........常用基准级数几何级数若数列{an}是公比为q的等比数列an=a1qn−1,a1̸=0,则级数∞∑n=1an称为几何级数(又称等比级数).p级数1+12p+13p+···+1np+···(p>0).当p>1时,该级数收敛;当p≤1时,该级数发散........(3)比值审敛法、根...