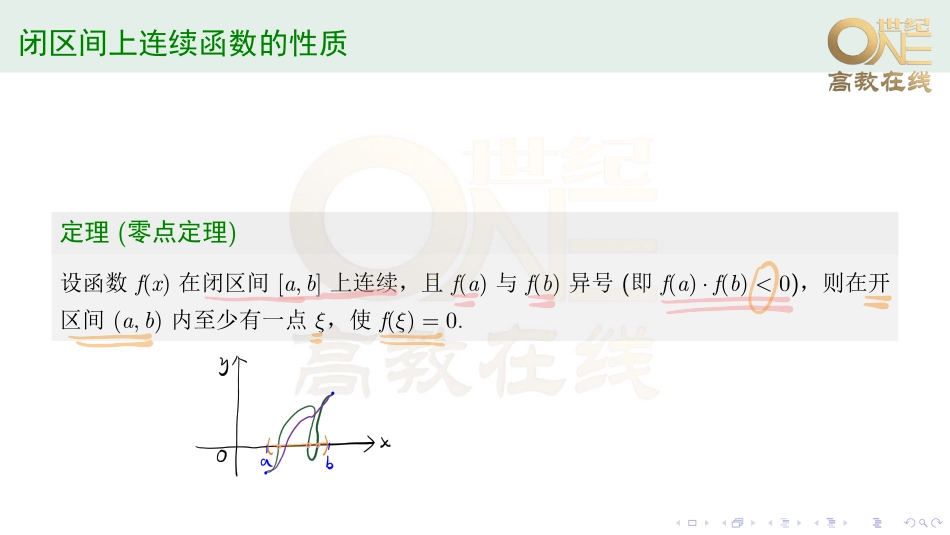
......Day12:闭区间上连续函数的性质......闭区间上连续函数的性质定义(最大值、最小值)对于在区间I上有定义的函数f(x),若存在x0∈I,使得对于任一x∈I都有f(x)≤f(x0)(f(x)≥f(x0)),则称f(x0)是函数f(x)在区间I上的::最::大::::::值(最:::小:::值).定理(有界性与最值定理)在闭区间上连续的函数在该区间上有界且一定能取得它的最大值和最小值.......闭区间上连续函数的性质定理(零点定理)设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号(即f(a)·f(b)<0),则在开区间(a,b)内至少有一点ξ,使f(ξ)=0.......闭区间上连续函数的性质定理(介值定理)设函数f(x)在闭区间[a,b]上连续,且在这区间的端点取不同的函数值f(a)=A,f(b)=B,则对于A与B之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得f(ξ)=C(a<ξ0,a̸=1)(10)(ex)′=ex(11)(logax)′=1xlna(a>0,a̸=1)(12)(lnx)′=1x(13)(arcsinx)′=1√1−x2(14)(arccosx)′=−1√1−x2(15)(arctanx)′=11+x2(16)(arccotx)′=−11+x2......单侧导数左导数f′−(x0)=limh→0−f(x0+h)−f(x0)h;右导数f′+(x0)=limh→0+f(x0+h)−f(x0)h.函数f(x)在点x0处可导的充分必要条件是左导数与右导数都存在且相等.......【例】设f(x)可导,F(x)=f(x)(1+|sinx|),则f(0)=0是F(x)在x=0处可导的()(A)充分必要条件.(B)充分条件但非必要条件.(C)必要条件但非充分条件.(D)既非充分条件又非必要条件.............Day14:导数的几何意义......导数的几何意义函数y=f(x)在点x0处的导数f′(x0)在几何...