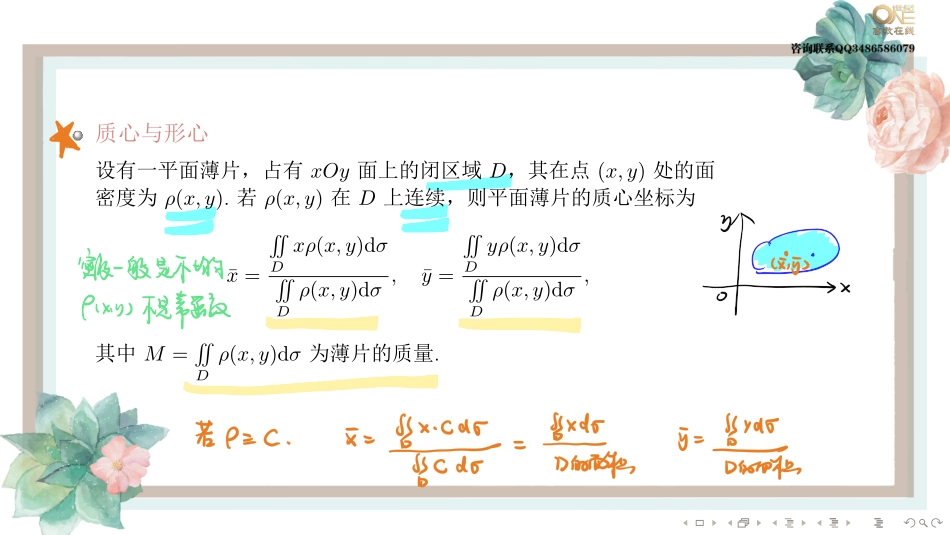
........第四节重积分的应用平面图形的面积空间立体的体积物体的质量质心与形心曲面的面积.......平面图形的面积与空间立体的体积根据二重积分的几何意义,平面区域D的面积等于˜Ddxdy,而以曲面z=f(x,y)为顶,区域D为底,D的边界为准线,母线平行于z轴的曲顶柱体的体积为˜Df(x,y)dxdy.空间立体Ω的体积等于˝Ωdv........质心与形心设有一平面薄片,占有xOy面上的闭区域D,其在点(x,y)处的面密度为ρ(x,y).若ρ(x,y)在D上连续,则平面薄片的质心坐标为¯x=˜Dxρ(x,y)dσ˜Dρ(x,y)dσ,¯y=˜Dyρ(x,y)dσ˜Dρ(x,y)dσ,其中M=˜Dρ(x,y)dσ为薄片的质量........类似地,占有空间有界闭区域Ω,在点(x,y,z)处的密度为ρ(x,y,z)(假定ρ(x,y,z)在Ω上连续)的物体的质心坐标为¯x=1M˚Ωxρ(x,y,z)dv,¯y=1M˚Ωyρ(x,y,z)dv,¯z=1M˚Ωzρ(x,y,z)dv,其中M=˝Ωρ(x,y,z)dv为物体的质量.均匀薄片的质心也是该平面薄片所占平面图形的形心;同理,均匀物体的质心也是该物体所占空间立体的形心.........例15..求心形线r=a(1+cosθ)(a>0)所围图形的形心................例16..球心在原点、半径为R的球体,在其上任意一点的密度的大小与这点到球心的距离成正比,求这球体的质量........曲面的面积设曲面S由方程z=f(x,y)给出,Dxy为曲面S在xOy面上的投影区域,函数f(x,y)在Dxy上具有连续偏导数f′x(x,y),f′y(x,y),则曲面的面积为A=¨Dxy√1+[f′x(x,y)]2+[f′y(x,y)]2dxdy.����见讲义第四节同步习题.