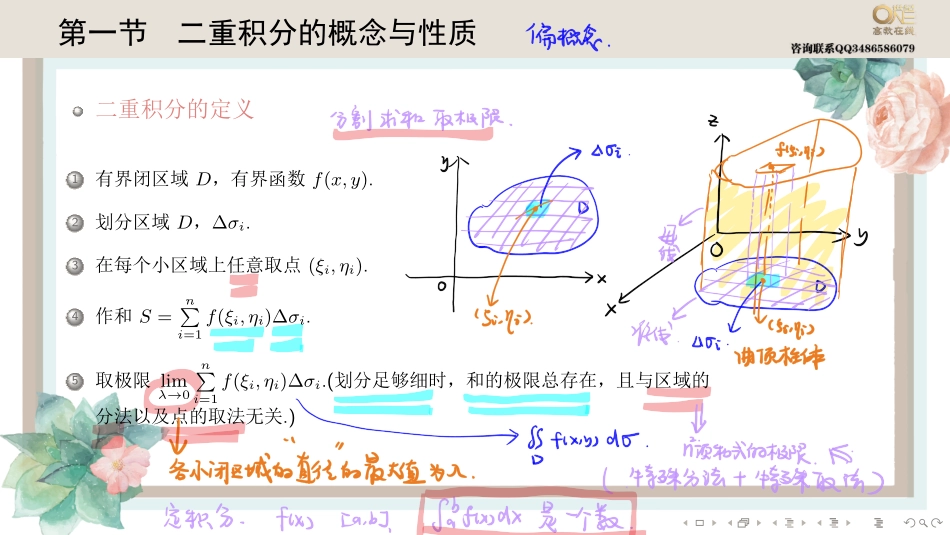
........第五章重积分.1二重积分的概念与性质.2二重积分的计算.3三重积分.4重积分的应用........第一节二重积分的概念与性质二重积分的定义.1有界闭区域D,有界函数f(x,y)..2划分区域D,∆σi..3在每个小区域上任意取点(ξi,ηi)..4作和S=n∑i=1f(ξi,ηi)∆σi..5取极限limλ→0n∑i=1f(ξi,ηi)∆σi.(划分足够细时,和的极限总存在,且与区域的分法以及点的取法无关.)........例1..limn→∞n∑i=1n∑j=1n(n+i)(n2+j2)=()(A)´10dx´x01(1+x)(1+y2)dy.(B)´10dx´x01(1+x)(1+y)dy.(C)´10dx´101(1+x)(1+y)dy.(D)´10dx´101(1+x)(1+y2)dy........二重积分的几何意义二重积分˜Df(x,y)dσ表示的是以区域D为底,曲面z=f(x,y)(注意:这里要求f(x,y)非负并且在D上连续)为顶的曲顶柱体的体积,该曲顶柱体的准线是D的边界,母线平行于z轴........二重积分与定积分被积函数积分区域(区间)积分变量积分和几何意义´baf(x)dxf(x)有界[a,b]xn∑i=1f(ξi)∆xi曲边梯形面积˜Df(x,y)dσf(x,y)有界Dx,yn∑i=1f(ξi,ηi)∆σi曲顶柱体体积二重积分的性质(1)设α与β为常数,则¨D[αf(x,y)+βg(x,y)]dσ=α¨Df(x,y)dσ+β¨Dg(x,y)dσ........(2)若闭区域D被有限条曲线分为有限个部分闭区域,则在D上的二重积分等于在各部分闭区域上的二重积分之和.(3)若在D上,f(x,y)=1,S为D的面积,则S=¨D1dσ=¨Ddσ.(4)若在D上,f(x,y)≤g(x,y),则有¨Df(x,y)dσ≤¨Dg(x,y)dσ........(5)设M和m分别是f(x,y)在闭区域D上的最大值和最小值,σ是D的面积,则有mσ≤¨Df(x,y)dσ≤Mσ.(6)二重积分的中值定理设函数f(x,y)在闭区域D上连续,σ是D的面积,则D上至少存在一点(ξ,η),使得¨Df(x,y)dσ=f(ξ,η)σ.........例2..设f(x,y)在D={(x,y)|x2+y2≤a2}上连续,则lima→01a2˜Df(x,y)dσ()(A)不一定存在.(B)存在且等于f(0,0).(C)存在且等于πf(0,0).(D)存在且等于1πf(0,0)........二重积分的积分区域关于坐标轴对称设f(x,y)是有界闭区域D上的连续函数,则有如下结论.1⃝当积分区域D关于y轴对称时,•若f(x,y)为关于x的奇函数,即f(−x,y)=−f(x,y),则˜Df(x,y)dσ=0.•若f(x,y)为关于x的偶函数,即f(−x,y)=f(x,y),则˜Df(x,y)dσ=2˜D1f(x,y)dσ,其中D1为D在x≥0半平面上的部分.2⃝当积分区域D关于x轴对称时,有类似结论(见讲义).........例3..设区域D={(x,y)||x|+|y|≤1}.D1是D在第一象限内的部分.f(x,y)在D上连续,等式˜Df(x,y)dxdy=4˜D1f(x,y)dxdy成立的充分条件是()(A)f(−x,−y)=f(x,y).(B)f(−x,−y)=−f(x,y).(C)f(−x,y)=f(x,−y)=−f(x,y).(D)f(−x,y)=f(x,−y)=f(x,y)................例4..如图,正方形{(x,y)||x|≤1,|y|≤1}被其对角线划分为四个区域Dk(k=1,2,3,4),Ik=˜Dkycosxdxdy,则max1≤k≤4{Ik}=()(A)I1.(B)I2.(C)I3.(D)I4........����见讲义第一节同步习题.