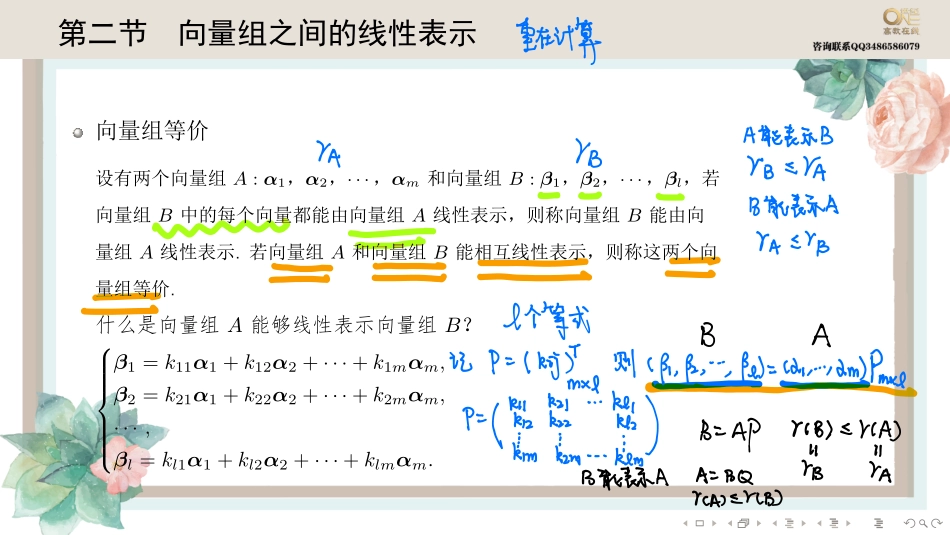
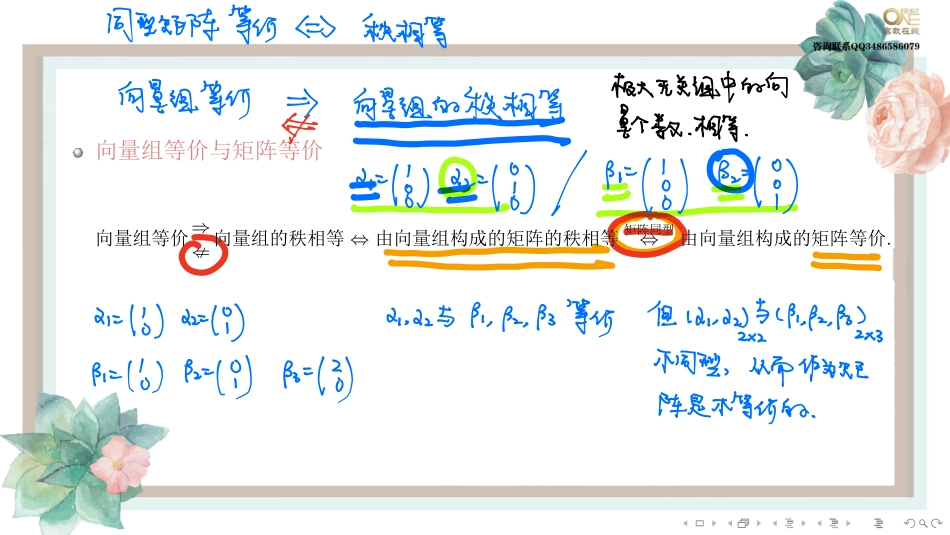
........�������������������������A:α1�α2�···�αm����B:β1�β2�···�βl�����B������������A����������B�����A����.����A����B������������������.������A���������B������������β1=k11α1+k12α2+···+k1mαm,β2=k21α1+k22α2+···+k2mαm,···,βl=kl1α1+kl2α2+···+klmαm.重在计算诉污邀阙1313能表示AVANBl个等式BA记Pkji则lffi.pe2⼩川Pmxemxf叫嚣嚣䉭13ApriBIENA13能表示AABQ管总rcmEnB.......���������������⇒⇍�������⇔�����������������⇔�����������.同型矩阵等何⼼秋相骂极⼤⽆关诅中的向向量组等何并向是组的秋鹕是个数相等州⻔州⻔州Big21216⼼DmypigBy了新但以1.22与⼼冷是不同型叕⽽作为矩阵是不等价的.......���������β�����α1�α2�···�αl����⇔����k1�k2�···�kl���k1α1+k2α2+···+klαl=β⇔���Ax=β�����A=(α1,α2,···,αl)⇔r(α1,α2,···,αl)=r(α1,α2,···,αl,β).��������������������������.ifōili蹨rm2essrchdz北B重点ha22北3ha222bB来⾃p可由⼩2⼀⼭表示CsruinAP没有加⼊新东⻄.......�������������β1�β2�···�βm�����α1�α2�···�αl����⇔��l×m��P���(β1,β2,···,βm)=(α1,α2,···,αl)P⇔����(α1,α2,···,αl)X=(β1,β2,···,βm)�����X�l×m��⇔r(α1,α2,···,αl)=r(α1,α2,···,αl,β1,β2,···,βm).PliknhtkzaznnkeldtBiRiz2itkzz2zttkhat记管良⾔热点kmihikmhtkzmhttkemMCRfipm⼆⽇北P矩阵⽅程P为该⽅程的解显然ha⼈北rcaaz--2efi-Pm重点⼩⼈北3rcaazaen_nPi㗅能由前⾏表示相当于没加新东⻄.......�������������������β1�β2�···�βm����α1�α2�···�αl�������������⇔����(α1,α2,···,αl)X=(β1,β2,···,βm)�(β1,β2,···,βm)Y=(α1,α2,···,αl)���⇔r(α1,α2,···,αl)=r(β1,β2,···,βm)=r(α1,α2,···,αl,β1,β2,···,βm).�����m=l�����������m�����Q���(β1,β2,···,βm)=(α1,α2,...