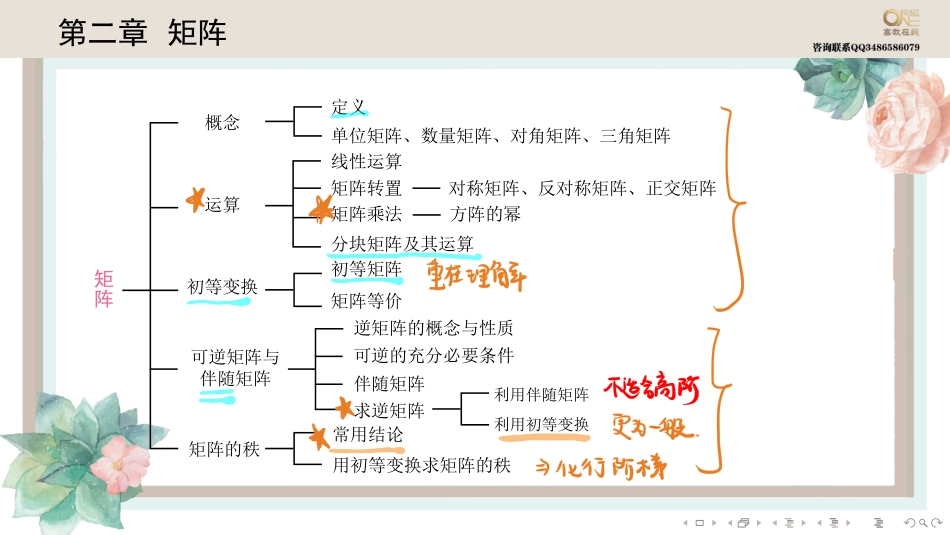
........第二章矩阵�����������������������������������������������������������������������������������������������������������������������������������������������........第一节矩阵的运算与变换矩阵由m×n个数aij(i=1,2,···,m;j=1,2,···,n)排成的m行n列的数表a11a12···a1na21a22···a2n.........am1am2···amn称为m行n列矩阵,简称为m×n矩阵,记作A=a11a12···a1na21a22···a2n.........am1am2···amn........矩阵的线性运算.1矩阵的加法交换律A+B=B+A.结合律(A+B)+C=A+(B+C)..2矩阵的数乘结合律(λµ)A=λ(µA).分配律1(λ+µ)A=λA+µA.分配律2λ(A+B)=λA+λB........矩阵的转置把矩阵A的行换成同序数的列得到一个新矩阵,叫做A的转置矩阵,记作AT.矩阵转置的运算律见讲义.方阵的行列式由n阶方阵A的元素所构成的行列式(各元素的位置不变),称为方阵A的行列式,记作detA或|A|.方阵的行列式的性质见讲义........矩阵乘法设A=(aij)是一个m×s矩阵,B=(bij)是一个s×n矩阵,那么规定矩阵A与矩阵B的乘积是一个m×n矩阵C=(cij),其中cij=ai1b1j+ai2b2j+···+aisbsj=s∑k=1aikbkj(i=1,2,···,m;j=1,2,···,n),并把此乘积记作C=AB.结合律1(AB)C=A(BC).结合律2λ(AB)=(λA)B=A(λB)(其中λ为数).分配律A(B+C)=AB+AC;(B+C)A=BA+CA........矩阵的乘法不满足交换律,即在一般情形下,AB̸=BA.矩阵的乘法也不满足消去律,即AB=AC,A̸=O⇏B=C.同理,BA=CA,A̸=O⇏B=C.特别地,AB=O⇏A=O或B=O,即两个非零矩阵的乘积可能为零矩阵........方阵的幂设A为n阶方阵,定义A1=A,A2=A1A1,···,Ak+1=AkA1,其中k为正整数,即Ak为k个A连乘..1与对角矩阵有关的高次幂.2与αβT有关的高次幂.3与幂零矩阵有关的高次幂.......若A为对角矩阵diag{λ1,λ2,···,λn},则Ak=diag{λk1,λk2,···,λkn}.若A为可相似对角化的矩阵,即存在可逆矩阵P,使得P−1AP=Λ,则A=PΛP−1,An=PΛnP−1.若A=αβT,其中α,β为n维列向量,则An=αβTαβT···αβT����n个αβT=α(βTα···βTα����n−1个βTα)βT=(βTα)n−1αβT.注意:这里αβT是n阶矩阵,但βTα是一个数,且等于αβT的主对角线之和,即αβT的迹........幂零矩阵若存在正整数k...