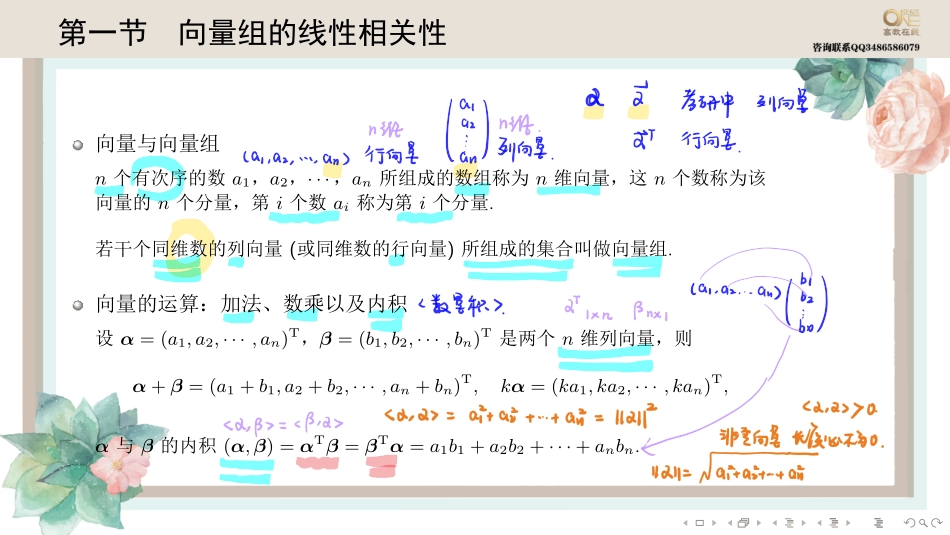
........第三章向量�����������������������������n���������������������������������������������������������������������������������������������������������������........第一节向量组的线性相关性向量与向量组n个有次序的数a1,a2,···,an所组成的数组称为n维向量,这n个数称为该向量的n个分量,第i个数ai称为第i个分量.若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组.向量的运算:加法、数乘以及内积设α=(a1,a2,···,an)T,β=(b1,b2,···,bn)T是两个n维列向量,则α+β=(a1+b1,a2+b2,···,an+bn)T,kα=(ka1,ka2,···,kan)T,α与β的内积(α,β)=αTβ=βTα=a1b1+a2b2+···+anbn........线性组合给定向量组A:α1,α2,···,αm,对于任何一组实数k1,k2,···,km,表达式k1α1+k2α2+···+kmαm称为向量组A的一个线性组合,k1,k2,···,km称为这个线性组合的系数.向量组线性相关给定向量组A:α1,α2,···,αm.若存在不全为零的数k1,k2,···,km,使得k1α1+k2α2+···+kmαm=0,则称向量组A是线性相关的,否则称它是线性无关的........两个3维向量线性相关的几何意义是两向量共线.三个3维向量线性相关的几何意义是三向量共面.对于只含一个向量α的向量组,当α=0时是线性相关的,当α̸=0时是线性无关的.对于含有两个非零向量α1,α2的向量组,其线性相关的充分必要条件是α1,α2的分量对应成比例.若向量组中有零向量,则该向量组必线性相关.........例1..n维向量组α1,α2,···,αs(3≤s≤n)线性无关的充分必要条件是()(A)存在一组不全为零的数k1,k2,···,ks,使k1α1+k2α2+···+ksαs̸=0.(B)α1,α2,···,αs中任意两个向量都线性无关.(C)α1,α2,···,αs中存在一个向量,它不能用其余向量线性表出.(D)α1,α2,···,αs中任意一个向量都不能用其余向量线性表出.........例2..举例说明下列各命题是错误的:(1)若向量组α1,α2,···,αm是线性相关的,则α1可由α2,···,αm线性表出;(2)若有不全为0的数λ1,λ2,···,λm,使λ1α1+···+λmαm+λ1β1+···+λmβm=0成立,则α1,···,αm线性相关,β1,···,βm亦线性相关;........例2..(3)若只有当λ1,λ2,···,λm全为0时,等...