数字信号处理_4 快速卷积.pptVIP免费

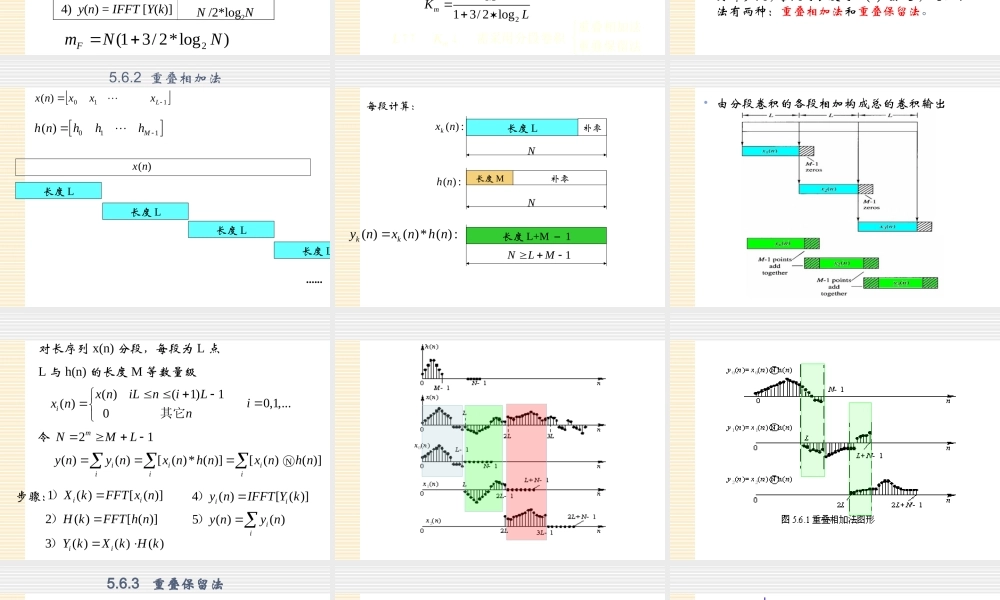
5.6线性卷积的FFT算法——快速卷积概述•线性卷积是求离散系统响应的主要方法之一,许多重要应用都建立在这一理论基础上,如卷积滤波等。•圆周卷积是唯一能借助计算机以提高运算速度的卷积运算•当满足一定条件时可以用圆周卷积实现线性卷积5.6.1FFT的快速卷积算法dmLM直接计算的乘法运算量为：若L点x(n)，M点h(n)，则直接计算其线性卷积y(n)10()()()Mmynhmxnm利用计算机快速计算线性卷积，即算圆周卷积：补零至N求FFT补零至N求FFT)()()(kHkXkY求IFFTFFT法：以圆周卷积代替线性卷积21mNML()01()01xnnLxnLnN()01()01hnnMhnMnNN()()*()()()ynxnhnxnhn()()()ynxnhnN令则2(13/2*log)FmNNN/2*log2NN/2*log2NNN/2*log2N1)H(k)=FFT[h(n)]2)X(k)=FFT[x(n)]3)Y(k)=H(k)X(k)4)y(n)=IFFT[Y(k)]计算量（复数乘法）：补零至N求FFT补零至N求FFT)()()(kHkXkY求IFFT()()()ynxnhnN比较直接计算和FFT法计算的运算量2(13/2*log)dmFmMLKmNN2225/23/2*log53logmMMKMM（）213/2logmMKL讨论：ML12NMLM则1）当LM1NMLL则2）当mLK需采用分段卷积重叠相加法重叠保留法•x(n)、h(n)两序列长度比较接近或相等的时候可以用圆周卷积计算线性卷积;•如果x(n)、h(n)长度相差较多,例如,h(n)为某滤波器的单位脉冲响应,长度有限,用来处理一个很长的输入信号x(n),或者处理一个连续不断的信号，按上述方法,h(n)要补许多零再进行计算,计算量有很大的浪费，或者根本不能实现。•为了保持快速卷积法的优越性,可将x(n)分为许多段,每段的长度与h(n)接近,处理方法有两种：重叠相加法和重叠保留法。110)(Lxxxnx011()Mhnhhh长度L)(nx......长度L长度L长度L5.6.2重叠相加法长度L:)(nxk:)(nh长度M()()*():kkynxnhn长度L+M－11NLMN补零N补零每段计算：•由分段卷积的各段相加构成总的卷积输出21mNML0,1,...i()(1)1()0ixniLniLxnn其它()()[()*()][()()]iiiiiiynynxnhnxnhnN1()[()]iiXkFFTxn）2()[()]HkFFThn）3()()()iiYkXkHk）4()[()]iiynIFFTYk）5()()iiynyn）对长序列x(n)分段，每段为L点L与h(n)的长度M等数量级令步骤：•将x(n)分为相互重叠的、长为L的子段xk(n)，每个子段不补零，直接作N=L圆周卷积，将结果中的前M1个不等于线性卷积值的点直接舍去...