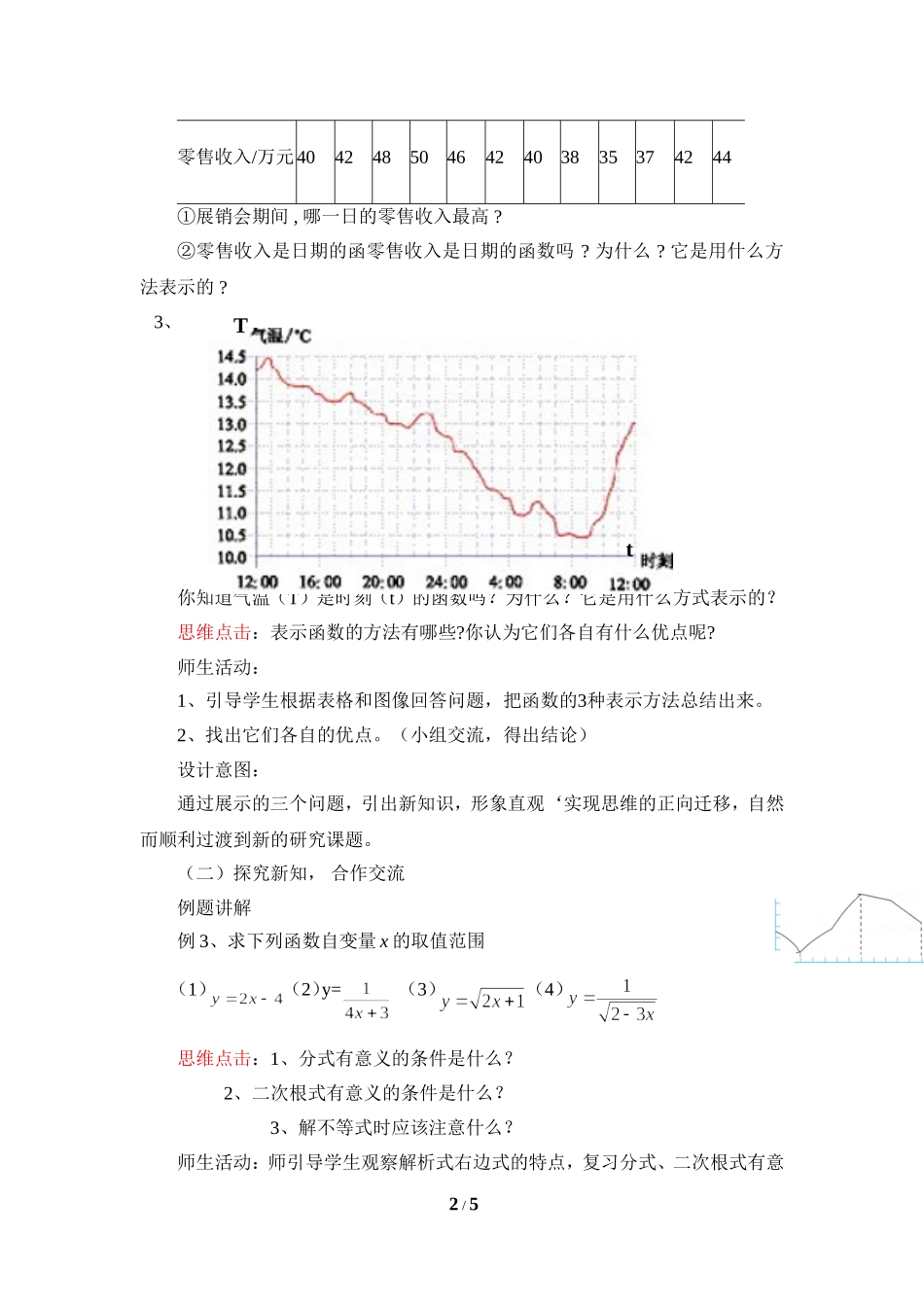
3.1对函数的再认识(2)一、教学目标:1、知识目标:学会用三种表示方法表示函数,能根据实际问题的意义及函数关系式,确定函数的自变量的取值范围,使学生进一步理解函数的意义。2、能力目标:使学生会根据实际问题求出函数的关系式。培养学生类比和转化的思想方法,锻炼学生独立的思考能力、缜密的逻辑思维能力和观察归纳的能力。3、情感目标:培养学生理论联系实际的科学态度。通过创设愉悦的学习情境使学生自始至终处于积极思考、大胆置疑、勇于创新、合作学习的氛围中,从而提高学习兴趣和教学效益。二、教学重点:会用三种表示方法表示函数,会求简单函数的自变量的取值范围。教学难点:会根据实际问题求出函数的关系式。三、教学方法:为使课堂有趣、生动和高效,结合本节课内容和学生的实际情况,采用引导发现和设疑诱导的教学方法。在教学过程中,通过创设富有启发性和研究性的问题情景,激发学生对问题的猜想和思考,激发学生探求知识的欲望,自觉地经历从发现问题到解决问题的过程。并使学生始终处于主动探索新知的积极状态,使其获取新知识的能力得到提高。四、教学用具:多媒体五、教学过程:(一)创设情景,引入新课出示问题:1、上节课我们学习的函数都是用数学式子表示的,你知道函数还可以怎么表示吗?2、某届全国图书展销会于5月份举行。本届书市总收入约1800万元(包括批发和零售),其中零售收入约500万元展销会期间的零售收入统计如下:日期/日1213141516171819202122231/5零售收入/万元404248504642403835374244①展销会期间,哪一日的零售收入最高?②零售收入是日期的函零售收入是日期的函数吗?为什么?它是用什么方法表示的?3、你知道气温(T)是时刻(t)的函数吗?为什么?它是用什么方式表示的?思维点击:表示函数的方法有哪些?你认为它们各自有什么优点呢?师生活动:1、引导学生根据表格和图像回答问题,把函数的3种表示方法总结出来。2、找出它们各自的优点。(小组交流,得出结论)设计意图:通过展示的三个问题,引出新知识,形象直观‘实现思维的正向迁移,自然而顺利过渡到新的研究课题。(二)探究新知,合作交流例题讲解例3、求下列函数自变量x的取值范围(1)(2)y=(3)(4)思维点击:1、分式有意义的条件是什么?2、二次根式有意义的条件是什么?3、解不等式时应该注意什么?师生活动:师引导学生观察解析式右边式的特点,复习分式、二次根式有意2/5Tt义的条件以及解不等式应注意的问题。例4:用总长为60m的篱...